Atunci când fasciculul de lumină este incident pe granița dintre cele două mass-media, există o reflectare a luminii: fasciculul își schimbă direcția de deplasare și se întoarce la mediul său original.
Fig. 4.2 prezintă incidentul ray AO, OB fasciculului reflectat și OC perpendicular, realizat de către suprafața reflectorizantă în punctul de incidență KL O.
Fig. 4.2. Legea de reflecție
Unghiul AOC numit unghiul de incidență. Acordați atenție și amintiți-vă: unghiul de incidență este măsurată de la perpendiculara pe suprafața reflectorizantă, și nu pe suprafața! In mod similar, unghiul de reflexie este unghiul BOC, format prin fasciculul reflectat și normala la suprafață.
4.2.1 Legea de reflecție
Acum am stat una dintre cele mai vechi legi ale fizicii. El a fost cunoscut de greci din antichitate!
1) fasciculul incident și fasciculul reflectat este perpendicular pe suprafața de reflexie, realizată de către punctul de minciună incidență într-un singur plan.
2) Unghiul de reflexie este egal cu unghiul de incidență.
Astfel, \ AOC = \ BOC, așa cum se arată în Fig. 4.2.
Legea reflexiei este un efect geometric simplu, dar foarte important. Să ne uităm la Fig. 4.3. Să emană din punctul de un fascicul de lumină. Un punct de construct 0. Un punct simetric în raport cu suprafața de reflexie a KL.
Fig. 4.3. Raza reflectată este emisă de la punctul A 0
Din simetria punctele A și A 0 clar că \ AOK = \ A 0 OK. Mai mult, \ AOK + \ AOC = 90. Prin urmare, \ A 0 OB = 2 (\ AOK + \ AOC) = 180. și, prin urmare, punctul A 0. O și B se află pe o linie dreaptă! OB fasciculului reflectat pe măsură ce merge de la punctul A la punctul simetric 0. A
în raport cu suprafața de reflexie. Acest fapt este foarte util pentru noi în viitorul foarte apropiat.
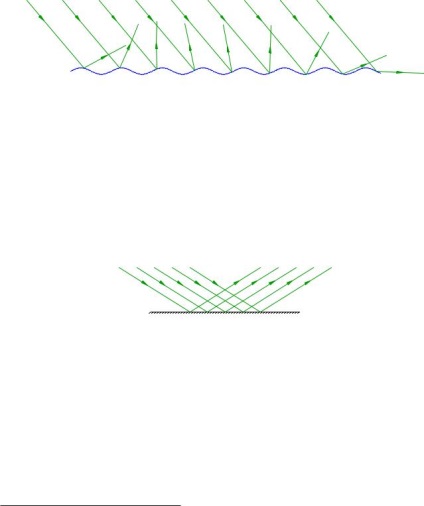
Legea de reflecție descrie cursul razelor de lumină individuale înguste Puchkov Sveta. Dar, în multe cazuri, fasciculul este larg suficient, care este compus dintr-o multitudine de raze paralele. Pictură fascicul reflecție largă va depinde de proprietățile suprafeței de reflexie.
În cazul în care suprafața este inegală, razele paralele după o reflecție este încălcată. Ca un exemplu, în Fig. 4.4 prezintă reflexia wavelike de la suprafață. Razele reflectate, după cum vom vedea, merge în multe direcții diferite.
Fig. 4.4. Reflexia de la o suprafață ondulată
Dar ce face ¾nerovnaya¿ suprafață? Ce suprafețe sunt ¾rovnymi¿? Răspunsul este că suprafața este considerată aspră, dacă mărimea rugozitatea nu este mai mică decât lungimea undelor luminoase. De exemplu, în Fig. 4.4 dimensiunea caracteristică a neregularităților de mai multe ordine de mărime mai mare decât lungimea de undă a luminii vizibile.
Suprafața cu neregularități microscopice proporționale cu lungimea de undă a luminii vizibile, numit mată. Ca urmare, fasciculul paralel reflectat de pe suprafața matted se obține lumina difuză a razelor luminoase care provin din toate direcțiile posibile 3. reflecție Inutil de la o suprafață este mata atât de dispersate sau difuze 4.
În cazul în care dimensiunea neregularităților de suprafață de mai mică decât lungimea de undă de lumină, atunci această suprafață se numește o oglindă. După reflexia din suprafața oglinzii paralelismului fasciculului este păstrată: razele reflectate merge, de asemenea, în paralel (figura 4.5.).
Fig. 4.5. Reflexia de la suprafața oglinzii
Aproximativ oglinda este suprafață netedă de apă, sticlă sau metal lustruit. Reflexia de la o suprafață de speculară este o oglindă, respectiv. Suntem interesați într-un caz special simplu, dar important reflexie a unei reflecție într-o oglindă plan.
4.2.2 Sticlă plană
Oglinda plană face parte dintr-o oglindă plan care reflectă lumina. oglindă plană lucru obișnuită; mai multe astfel de oglinzi în casa ta. Dar acum putem înțelege de ce, uita-te în oglindă, nu văd în ea o reflectare a ei înșiși și obiecte din jurul tău.
O sursă de lumină punctiformă S în Fig. 4.6 grinzi în direcții diferite; să luăm incidentul două raze vecine de pe oglinda plană. Știm deja că razele reflectate
3 De aceea vedem obiectele din jur: ele reflectă lumina ambientală pe care o vedem din orice unghi.
4 cuvânt latin di usio doar înseamnă distribuția, răspândirea, imprastiere.

vor fi utilizate ca și în cazul în care acestea provin de la un punct S 0. simmmetrichnoy punctul S în raport cu planul oglinzii.
Fig. 4.6. Imaginea sursei de lumină într-o oglindă plană
Distracția începe atunci când divergent reflectat razele vin la noi în ochi. Particularitatea mintea noastră este că creierul completează un fascicul divergent, continuând oglinda lui să se intersecteze într-un punct S 0. Se pare că razele reflectate emană de la punctul S 0, vom vedea că este un loc luminos!
Acest punct este imaginea sursei de lumină S. Desigur, în realitate, nimic nu în spatele oglinzii nu este aprins, nici o putere este concentrată este o iluzie, o iluzie optică, un produs al conștiinței noastre. Prin urmare, S 0 punct este numit sursa de imagine virtuală S. La punctul S 0 nu se intersectează razele de lumină și continuarea lor mentale ¾v zazerkale¿.
Este clar că imaginea S 0 va exista indiferent de mărimea oglinzii și dacă sursa este direct deasupra oglinzii sau nu (fig. 4.7). Este important ca razele reflectate de oglinda si intra in ochi astfel incat ochiul se va forma o imagine sursă.
Fig. 4.7. Sursa nu este deasupra oglinzii: există încă imagini
Din locația dimensiunea sursei și oglindă depinde regiune spațială regiune viziune, care arată imaginea sursă. Câmpul vizual dat de marginile de oglinzi K și L KL. Construcție a zonei de imagine vizibilitate S 0 este clar din Fig. 4.8; viziune de domeniu dorit evidențiate cu gri.
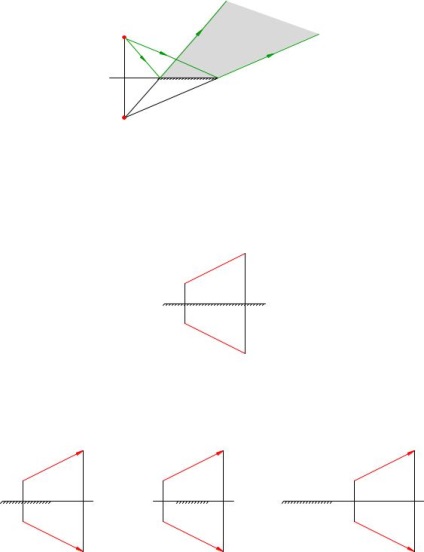
Fig. 4.8. regiunea viziune sursă de imagine S
Cum de a construi o imagine arbitrară a obiectului într-o oglindă plan? Pentru a face acest lucru, este suficient să se găsească o imagine a fiecărui punct al subiectului. Dar noi știm că imaginea unui punct simetric în raport cu însăși punctul oglinzii. Prin urmare, imaginea obiectului în oglindă plan obiect simetric în raport cu un plan oglindă (fig. 4.9).
Fig. 4.9. AB imagine obiect într-o oglindă plan
Locație obiect în raport cu oglinda și dimensiunea oglinzii nu afectează imaginea (Fig. 4.10).