Condiția necesară pentru convergența unui număr: Un număr poate fi de acord doar în cazul în care termenul său general tinde la 0 ca n
Un criteriu suficient pentru divergența seriei. În cazul în care termenul general nu tinde la 0 => diverge seria
Atenție: o condiție necesară = 0 nu este suficient pentru convergenta a seriei. Un număr de care. poate converge sau se pot abate.
Exemplul 1. Un număr de + 0,44 + 0,4 + 0,444 0.4444 + ...
divergenta, pentru că termen general nu tinde la 0.
Exemplul 2. Un număr de 1-1 + 1-1 + ...
diverge ca = Termenul general nu tinde la 0.
Și, în general, nu are nici o limită.
Exemplul 3. Mai multe divergenta ca
5) numărul + ... + numita serie de armonice este divergentă și următoare, deoarece secvența acesteia crește suma parțială pe termen nelimitat.
Ie convergența necesară a semnului face imposibil de a judeca dacă este sau nu seria converge. Convergență și divergență al seriei, în multe cazuri, pot fi stabilite cu dovezi suficiente de convergență.
Luați în considerare unele dintre ele pentru seria znakopolozhitelnyh, și anume pentru seriile cu termeni non-negativ (numărul znakootritsatelny de treceri în znakopolozhitelny prin înmulțirea cu (-1), care nu afectează convergența seriilor).
indicii suficiente de convergență
semn comparație serie
Convergența sau divergența unei serii znakopolozhitelnogo adesea stabilite prin compararea cu alții ( „de referință“) din apropiere, care este cunoscută pentru a converge sau nu.
„De referință“ sunt de multe ori sunt rânduri:
a) armonică serie - evazată sau
b) o progresie geometrică :.
· În cazul în care seria converge
· În cazul în care seria divergenta
· În cazul în care seria divergenta
Acesta poate fi scris după cum urmează:
=> Acest număr exponențial, în cazul în care a =
q = => această serie converge.
Teorema. două serii znakopolozhitelnyh Să presupunem că
Dacă inegalitatea n => convergența din al doilea rând trebuie să convergență din primul rând, primul rând de divergență urmează oa doua serie de divergență.
1) Pentru a investiga convergența seriilor
Să comparăm acest număr cu un număr de
serie progresie geometrică de ordine, care este convergent, ca q =
pentru că => Seria convergent.
2) Pentru a investiga convergența seriei:
Să comparăm acest număr cu seria armonică:
1+ serii divergente de ordine
pentru că fiecare => divergenta această serie
3) Pentru a investiga convergența seriilor
Comparabil cu un număr de progresie geometrică:
. care converge (q =
pentru că => Serialul converge
4) Convergența seriei: 1+
Compara cu o serie de exponențial
Teorema: Având în vedere un număr de znakopolozhitelny + ... și există o limită finită sau infinit
Apoi, seria converge <1; и расходится при>1
(If = 1, convergența rămâne nerezolvat)
(Testul D'Alembert este necesar să se aplice în cazul în care termenul general al seriei conține n! Or)
1) Pentru a investiga convergența seriilor
= => L = 0<1 =>această serie converge pe baza d'Alembert.
L = 3> 1 => număr pe baza D'Alembert diverge.
atribut Cauchy (radical)
Având în vedere un număr de
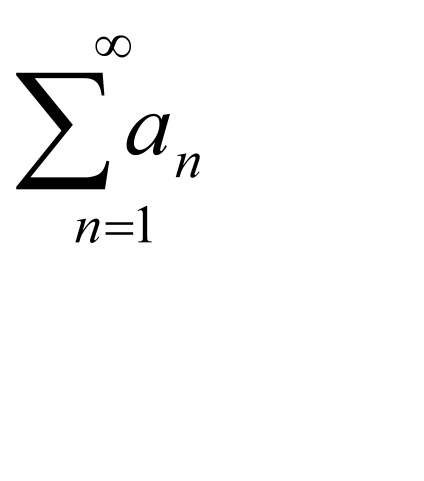
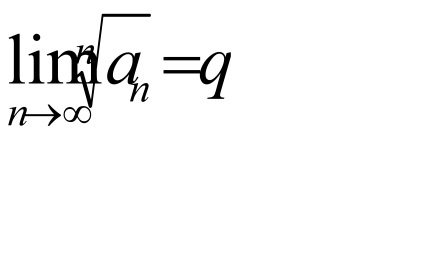
Dacă q> 1, atunci seria diverge.
Dacă q<1, то ряд сходится.
semnul lui Leibniz (pentru serii alternativ):
Seria convergent în cazul în care sunt îndeplinite două condiții:
1) numărul de elemente în mărime descrescătoare uniform;
2) limitează termenul general al seriei este zero.
Seria Power este o serie de forma
Pentru a găsi o serie de putere în intervalul de convergență este necesară pentru:
1) Testul d'Alembert de a aplica la rândul sau Cauchy asamblate din module;
2) examinează convergența seriilor pe capetele intervalului.
EXEMPLU 1.Issledovat intervalul de convergență
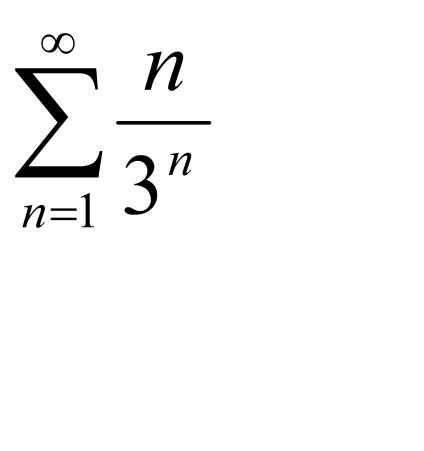
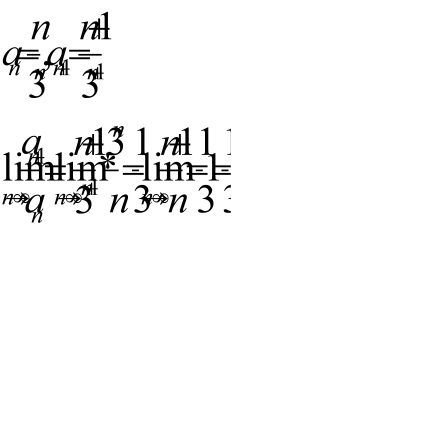
T. k.
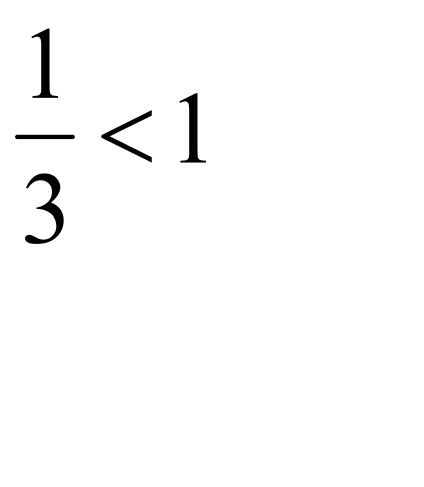
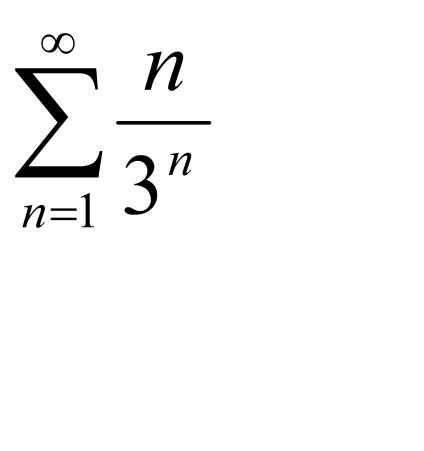
Exemplul 2. Exploreaza convergența seriilor
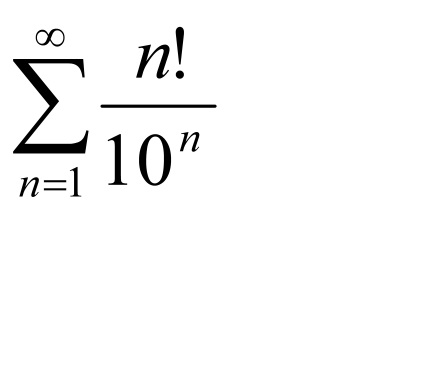
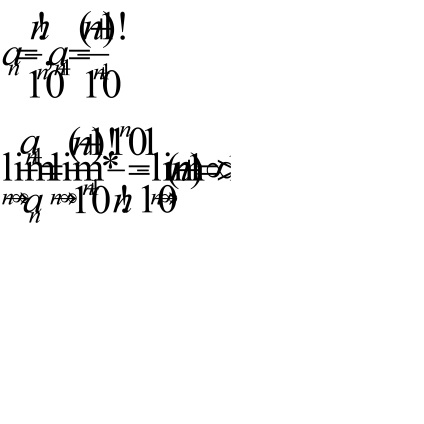
T. k.
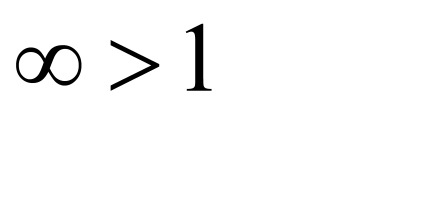
Exemplul 3. Testul pentru intervalul de convergență

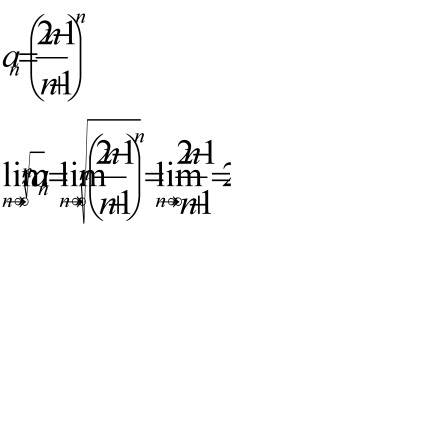
pentru că
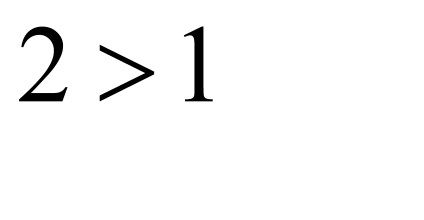
Exemplul 4 Folosind semnul Leibniz examinate pentru gama de convergență
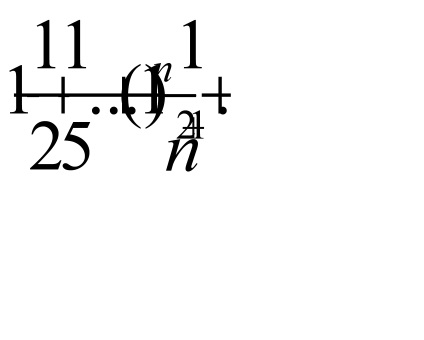
Deoarece membrii seriei în valoare absolută monoton
scădere
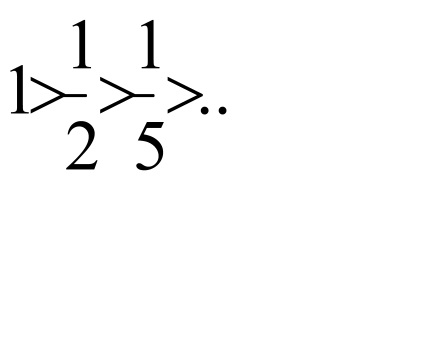
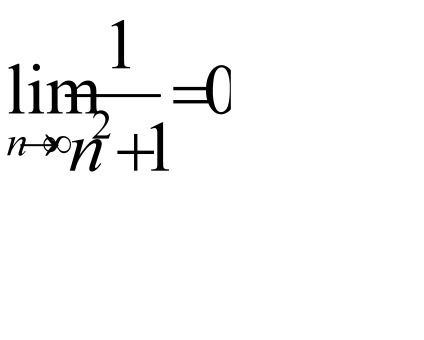
Exemplu 5.Issledovat convergența absolută și condiționată a serii:
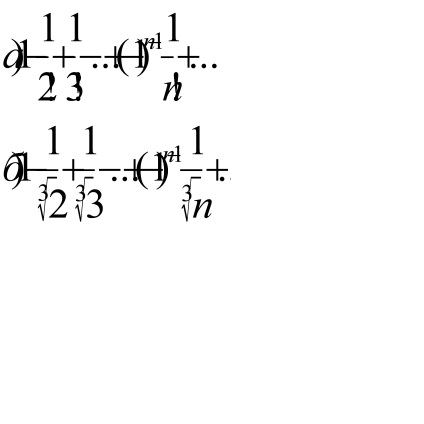
a) se consideră format din valorile absolute
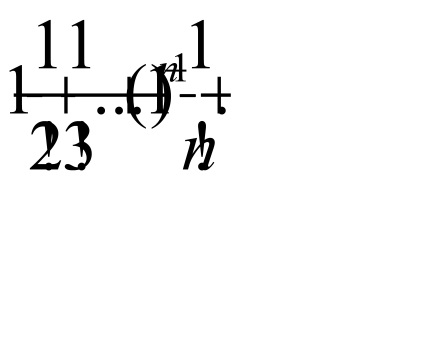
Pe baza d'Alembert această serie converge, din moment ce

Astfel, seria diverge complet.
b) Un număr format din valorile absolute ale termenilor seriei
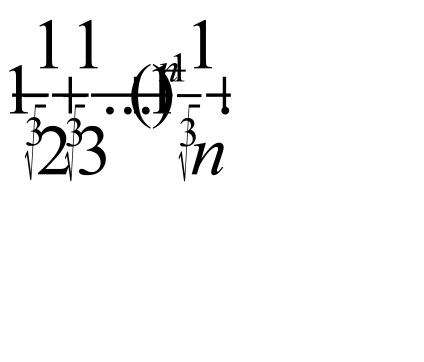
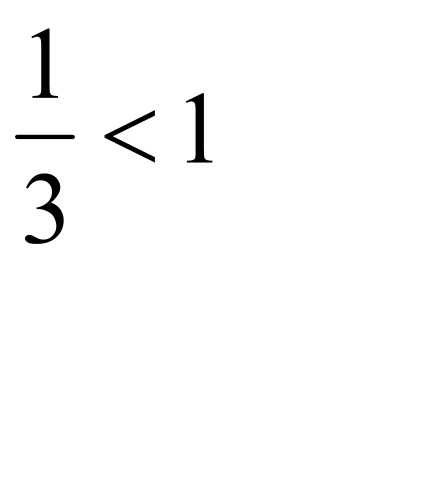
În consecință, seria originală nu este absolut convergentă.
L-am examinat pe convergența condiționată.
rând
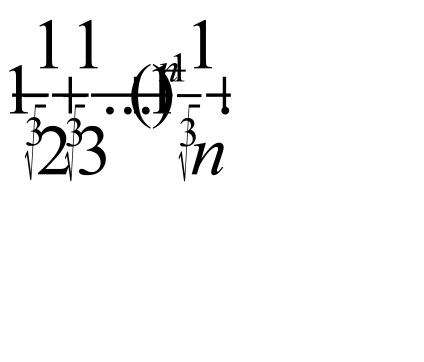
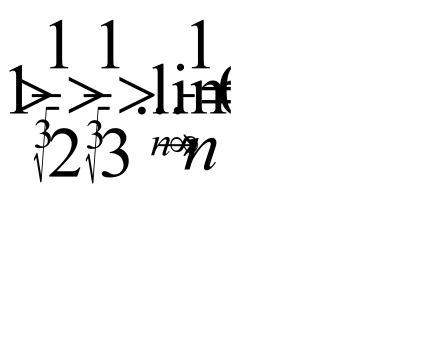
Deci seria converge în mod condiționat.
Exemplul 6. Găsiți domeniul de convergență al unei serii de puteri
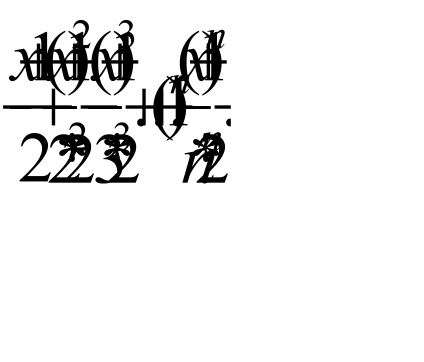
Luați în considerare format din valorile absolute
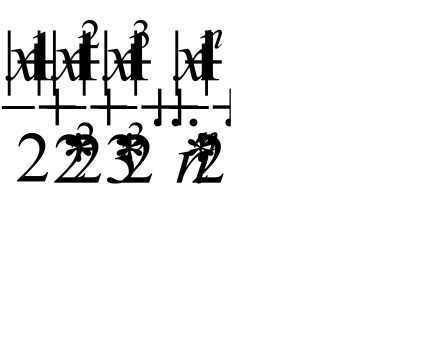
Pe baza d'Alembert

Luați în considerare inegalitatea
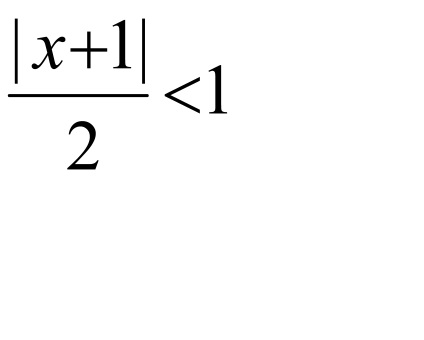
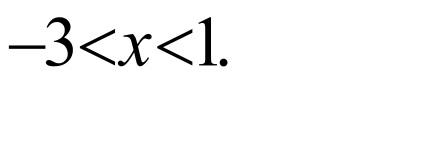
Noi examinăm convergența capetele diferenței.
Când x = -3 obține seria:
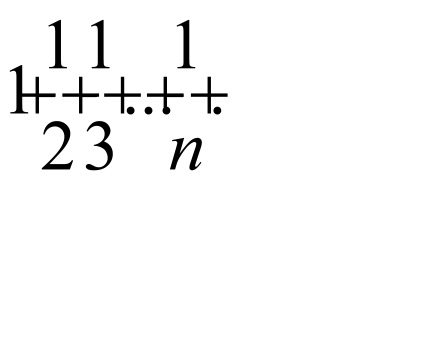
Când x = -3 obține seria:
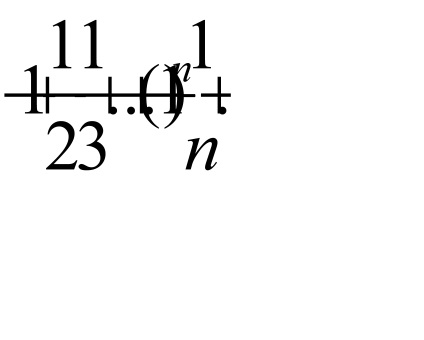
Astfel, intervalul de convergență a seriei este un decalaj
Exploreaza convergența seriei: