Modelarea sistemelor economice care utilizează procese Markov
Concepte de bază ale proceselor Markov
Pentru funcția aleatoare se numește, în cazul în care valoarea atunci când argumentul lu-BOM / este o variabilă aleatoare.
Funcția aleatorie a cărui argument este un timp, numit un proces stocastic.
procese Markov sunt un tip special de procese pro-aleatoare. Un loc special de procese Markov, printre alte clase de procese aleatorii se datorează următoarele circumstanțe: pentru procesele Markov sunt bine dezvoltate matematic AP-Paraty, care permite de a rezolva multe probleme practice; procese Markov zoaie-schyu poate fi descrisă (sau aproximate cu precizie, dar) comportament sisteme destul de complicate.
Definiția. proces aleator care apar în ka-Coy fie sistem S, este numit un proces Markov (sau proces fără efect secundar), în cazul în care are următoarea proprietate: pentru orice moment / 0, probabilitatea de orice stare a sistemului în viitor (cu /> / 0) depinde numai din starea sa în prezent (la / = / 0) și nu depinde de momentul și modul în care un sistem S-timp a venit în această stare.
Clasificarea proceselor Markov. procese aleatoare ing Clasificarea Markov se face în funcție de un caracter continuu sau discret de valori de continuitate set unei funcții X (t) și parametrul /.
Există următoarele tipuri principale de procese Markov:
• cu stări discrete și timp discret (lanț Markov);
• cu stare continuă și discret de timp (secventa-mar Markovian);
• cu stări discrete și timp continuu (lanț Markov non-discontinue);
• cu stări continue și timp continuu.
În această lucrare vom lua în considerare doar pro-Markov procese cu stări discrete Sb S2 ,. Sn.
starea C) AF. Markov prelucrează cu niyami discrete cuprinzând ilustrat în mod convenabil prin așa numitele stări ale graficului (Fig. 2.1), unde cercurile denotă stări Si, S2 ,. Sistemul S, și săgețile - posibile tranziții de la o stare la o stare-ence. Graficul marcat numai tranziții imediate și să nu se deplaseze prin alte state. Posibil pentru-cost implicate în aceeași stare descrie „buclă“, adică. E. o săgeată orientată dintr-un anumit stat la sine. Numărul de stări ale sistemului poate fi finit sau infinit (dar NYM cont). EXEMPLUL J grafic starea sistemului este prezentată în Figura 2.1.
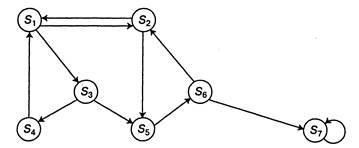
Fig. 2.1. Sistemul prevede S Count
Markov procese cu stări discrete și timp discret lanț Markov se numește. Pentru astfel de pro-cesiuni ori tx. t2 ,. 5, în cazul în care sistemul poate schimba starea sa-Yanie sunt considerate ca etape de proces succesive și onoruri ka-argument pe care procesul nu iese în afară de timp / și numărul pasul 1, la 2,. proces aleatoriu în acest caz ha secvență de stări 5 acterized (0) 5 (1) 5 (2). S (k). unde 5 (0) - Starea inițială a sistemului (înainte de prima etapă); 5 (1) - starea sistemului după prima etapă; S (k) - cu vivace sistem după etapa N-lea.
Eveniment care constă în faptul că, imediat după ce sistemul sha ha k este în stare 5 / (/ = 1, 2) este un eveniment caz-NYM. Secvență de stat 5 (0) 5 (1). 5 (). Acesta poate fi privit ca o secvență aleatoare Soby-rd. O secvență aleatorie de evenimente numite lanț Mar-bancar în cazul în care nu depinde de momentul și modul în care sistemul-MA a venit în 5 / pentru fiecare probabilitate de tranziție pas de lu-Dumnezeu stat 5 / la orice Sj. Inițială-stat 5 (0) poate fi predeterminat în avans sau aleatorii.
Probabilitățile de lanț Markov probabilitățile sunt numite cinci Pt (k), care, după k-pas (și înainte de (k + 1) -lea) sistem 5 va fi în starea 5, (/ = 1,2. N). Evident, pentru orice k
Distribuția inițială de probabilitate a lanțului Markov-numita INDICĂ distribuție de probabilitate a statelor de la începutul procesului:
În cazul particular când starea inițială a sistemului în punctul S-ness cunoscut S (0) = Sh atunci probabilitatea RDO inițială) = 1 și toți ceilalți sunt zero.
probabilitate de tranziție (probabilitate de tranziție) la etapa k de la stat Si la Sj de stat se numește probabilitatea condiționată ca primul, sistemul S, după k pas va fi în stare A atunci când YC-lovii care imediat înainte (după k - 1 pas) l-stat în hodilas 5 /.
Deoarece sistemul poate fi într-unul din n stări, atunci pentru fiecare dată / probabil nevoie pentru a seta n-stey tranziție Roux, care sunt prezentate în mod convenabil sub forma de matrice următoare:
unde - probabilitatea unei tranziții într-un pas de la starea Sj la S / statului - probabilitatea unui sistem întârziere în Sj de stat.
Matricea (2.3) se numește o matrice probabilitate de tranziție sau tranziție.
Dacă probabilitățile de tranziție nu sunt dependente de numărul pasului (timp), și depinde numai de ordinul unui stat în care tranziția este realizată, lanțul Markov corespunzător se numește, omogenitatea.
Probabilitățile de tranziție ale unui lanț Markov omogen Ru formează o matrice pătrată de note dimensiune nxn unele dintre caracteristicile sale .:
1. Fiecare rând caracterizează starea selectată a sistemului și elementele sale sunt probabilitățile tuturor tranzițiilor posibile cu un pas selectat dintre (a / th) de stat, inclusiv o tranziție în sine.
2. Elemente de coloane arată probabilitățile tuturor posibil sistem-TION merge pas cu pas (j-e) starea specificată (cu alte cuvinte, linia se referă la probabilitatea tranziției de la stat, coloana - în stare).
3. Suma probabilităților fiecărui rând este egal cu unitatea, așa cum tranzițiile formează un grup complet de evenimente incompatibile:
4. Pe diagonala principală a matricei probabilităților de tranziție sunt probabilitățile că sistemul este în afara statului și să rămână în ea.
Dacă un lanț Markov omogen este setat inițial probabilitate EFINIȚII Ras (2.2) și matricea de probabilitate de tranziție
(2.3), probabilitatea de stări ale sistemului sunt definite prin formula recurență:
Exemplul 2.1. Luați în considerare în procesul de funcționare a sistemului, am masina. Lăsați vehiculul (sistem) pentru CME-HN (zi) poate fi într-una din cele două stări: rectificat prin dl și defecte. starea sistemului Count este prezentat în Fig. 2.2.
Fig. 2.2. Count condiții auto
Ca urmare a observațiilor în masă pentru av-t o lucrare compilat următoarea matrice de probabilități de tranziție:
probabilitatea ca vehiculul va rămâne în stare bună;
probabilitatea de tranziție de la starea de masina „corecționale-vene“ în „defectiv“;
probabilitatea de tranziție de la starea mașinii, „Defect-vena“ la starea „OK“;
probabilitatea ca vehiculul va rămâne în starea „defect“.
Vectorul probabilităților inițiale ale vehiculului să poată solicita
Este necesar să se determine probabilitatea statelor vehiculului în trei zile.
Folosind o matrice de probabilități de tranziție, determinăm statele probabilitate yatnosti Pxx) după prima etapă (după prima zi):
Probabilitățile statelor după etapa a doua (după al doilea sous-curent) sunt:
probabilități de stat după a treia etapă (după a treia sous-curent) sunt egale
Astfel, după a treia zi masina este locat-ditsya în stare bună, cu o probabilitate de 0.819 în starea „defect“, cu o probabilitate de 0.181.
Exemplul 2.2. În timpul funcționării, calculatorul poate fi privit ca un sistem fizic-vatsya S, care, în rezultatul verificării poate fi într-una dintre următoarele stări:
Calculatoare complet de funcționare;
Calculatorul are un defect în memorie, cu Ko
toryh poate rezolva probleme;
-EVM are o problemă semnificativă și poate rezolva
clasă limitată de probleme;
-EVM complet de ordine.
La momentul inițial de timp computerul este complet reparat (cu picioare-Sx). Verificați computerul se face la luni- mente fixe de timp tb t2. ty proceselor care au loc în sistemul S, poate fi considerat ca fiind un lanț Markov omogen, cu trei trepte (primul, al doilea, al treilea calculator) verifică dacă există. probabilitate de tranziție Matrix-yatnostey este dată de:
Se determină probabilitatea unui stat calculator după trei controale.
Graficul stat are forma prezentată în Fig. 2.3. Împotriva săgeți-kazh doy din jurul probabilitatea de tranziție corespunzătoare. Probabilitățile inițiale ale statelor
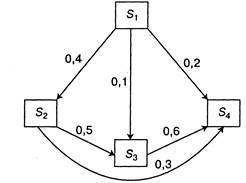
Fig. 2.3. Count state de calculator
În conformitate cu formula (2.5), luând în considerare suma probabilităților numai cei cu picioare, dintre care poate direcționa tranziția în această stare, găsim:
Deci, probabilitatea unui stat de calculator, după ce trei controale de pistă-ghiduri: