Formarea unui arbore ierarhic de clustere binare
Z = linkage (Y)
Z = linkage (Y, 'metodă')
= Linkage funcția Z (Y) permite să formeze un arbore ierarhic de clustering binar folosind un algoritm. Argumentul de intrare Y este un vector de distanțele dintre perechile de multitudinea de obiecte sursă de date în spațiul multidimensional. Numărul de elemente vector egal cu Y, în care: - numărul de obiecte din setul original de date. Y poate fi obținut ca o funcție de ieșire parametru pdist. În general, argumentul Y intrare poate fi definit ca o matrice de distanțele dintre perechile de pluralitatea inițiale a obiectelor de date, în funcție de formatul funcției de ieșire parametrul pdist.
parametru de ieșire Z este o matrice care conține informații despre arborele de cluster. Z este dimensiunea. Finite noduri de arbore de cluster sunt obiectele din setul original de date - observații cu variabile multiple variabila aleatoare Y, numerotate de la 1 la m. noduri finale sunt grupuri izolate. Ei grupate suprapusă noduri de arbore. Fiecare grup ulterior nod copac suprapusă corespunde rândul i-lea Z. matrice El este asociat cu indicele de m + i.
Coloanele 1 și 2 ale matricei Z conține indexuri de obiecte legate de noul cluster. Numărul clusterelor formate este egal cu binar (m-1).
coloana a 3-a Z matrice conține o valoare de distanțele dintre perechile de obiecte combinate în grupuri.
Să presupunem că clusterul conține 30 de colectare de semințe de copac. Dacă al 10-lea cluster-ul a fost format prin combinarea 5-lea și al 7-lea obiecte, iar între acestea distanța este de 1,5, atunci al 10-lea rând al Z matrice va conține următoarele valori Z (:, 10) = [6 mai 1.5]. Acest cluster va avea un indice de 10 + 30 = 40. În cazul în care codul 40 este detectat în liniile ulterioare Z, acest lucru înseamnă că 40 de cluster binar vor fi îmbinate într-un nou grup suprapusă.
Z = linkage (Y, 'metodă') argument de intrare 'metodă' permite specificarea unui algoritm de grupare. O „metodă“ de intrare valoare argument este definită ca o linie de test. Următorii algoritmi de clusterizare
unde, - r și s centroizi ale clusterelor.
Ca rezultat al algoritmului centroida nu poate fi obținut prin arborele de cluster monotonă. Această situație poate apărea atunci când distanța de la unirea a două clustere, al treilea grup este mai mică decât distanța de la r sau s k. În acest caz, dendrogramei poate schimba direcția sa, care este motivul pentru utilizarea unui algoritm de grupare diferită.
în care: - distanța dintre clusterii r și s, este determinată de un algoritm centroid. Algoritmul Incremental se bazează pe creșterea sumei totale de pătrate în interiorul grupului grupurile de aderare r și s. Suma intra-grup de pătrate este suma pătratelor distanțelor dintre toate obiectele din cluster și centroidului cluster.
Exemple de utilizare a funcției de formare a unui arbore ierarhic de clustere binare
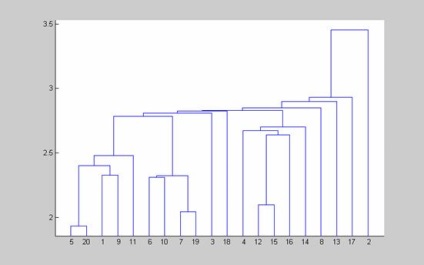
1. Formarea arborelui binar de clustere ierarhice pentru o variabilă aleatoare distribuită în mod normal, 10-dimensional. Numărul de obiecte dintr-un set de date de intrare este de 20. O reprezentare grafică a arborelui de cluster binar este realizată folosind funcția dendrogram.
2. Formarea arborelui binar de clustere ierarhice pentru variabila aleatoare bidimensionala. Numărul de obiecte din setul de date sursă este egal cu 7. sunt comparate diverși algoritmi de grupare. O reprezentare grafică a rezultatelor gruparea realizată prin dendrogram funcției.
2.1. Context:
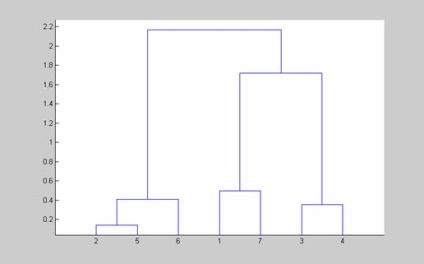
2.2. Clustering folosind un algoritm
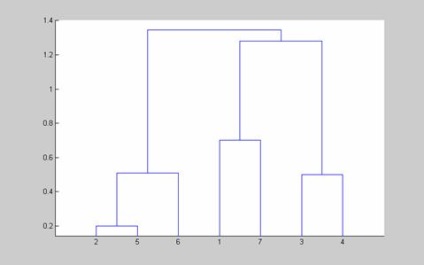
2.3. Clustering folosind un algoritm
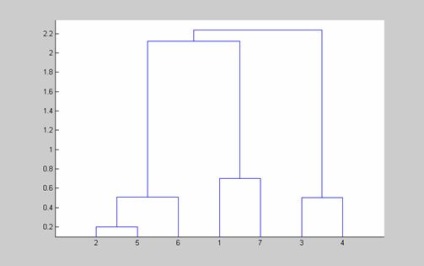
2.4. Clustering folosind un algoritm
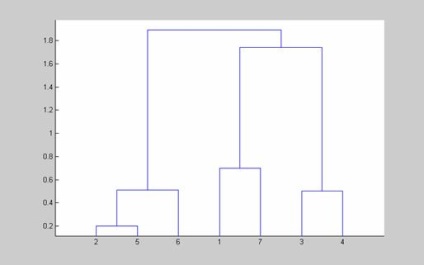
2.5. Algoritmul clustering folosind algoritmul centroida
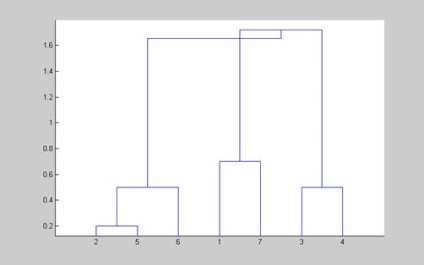
2.6. Algoritmul clustering folosind algoritmul incremental