Triangle. Centrul de greutate se află la intersecția medianele sale. Din geometria este cunoscut faptul că medianele triunghiului se intersectează într-un punct și sunt împărțite într-un raport de 1: 2 de la bază.
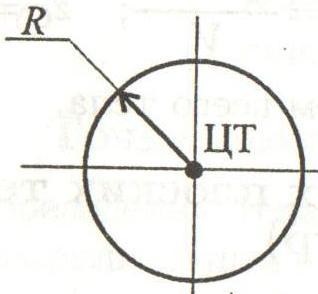
Cercul. Deoarece cercul are două axe de simetrie, centrul de greutate se află la intersecția axelor de simetrie.
Semicircle. Semicercul are o axă de simetrie, centrul de greutate se află pe această axă. Alte coordonate ale centrului de greutate se calculează cu formula :.
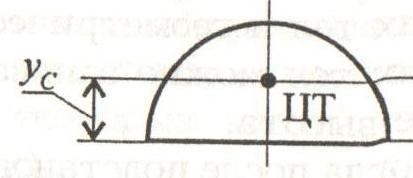
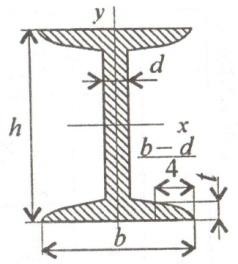
Multe componente sunt fabricate din standard, laminate - peste, I-grinzi, canale și altele. Toate dimensiunile, precum și caracteristicile geometrice ale secțiunilor laminate sunt date sub formă de tabele care pot fi găsite în cărțile de referință în tabelele de ecartament normal (GOST 8239-89, GOST 8240-89).
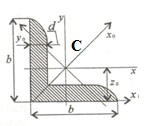
Exemplul 1. Pentru a determina poziția centrului de greutate al figurii prezentată în figură.
Am ales axele de coordonate, astfel încât axa x a trecut prin dimensiunile mai inferioare, iar axa y - la dimensiunile stânga.
Divizarea o figură complexă în numărul minim de forme simple:
Se calculează aria fiecărei forme simple, centrul de greutate coordonate. Rezultatele de calcul sunt înregistrate în tabel