problemă de programare convexă
2.1.1. Conceptul unui set convexe
Definiția. MnozhestvoS
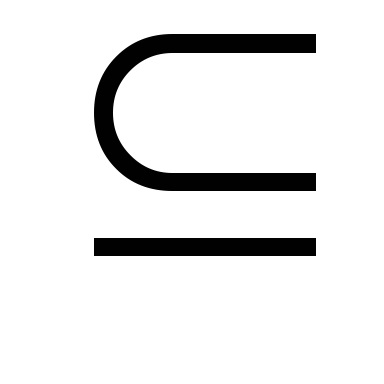

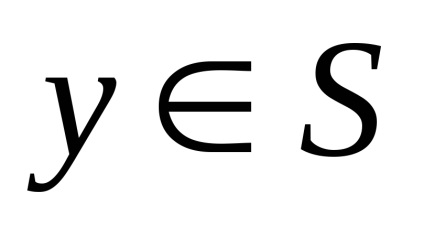
în orice
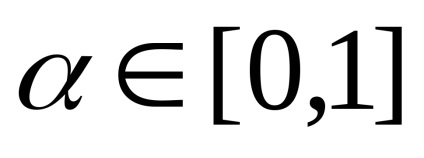
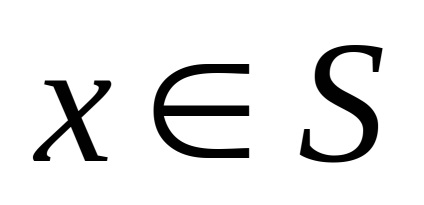
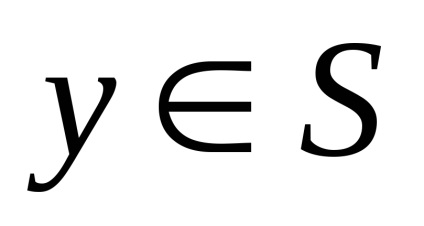
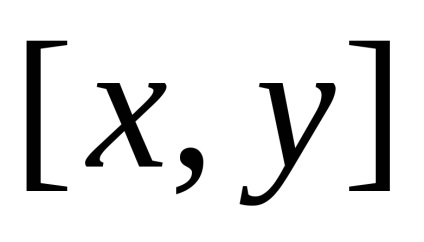


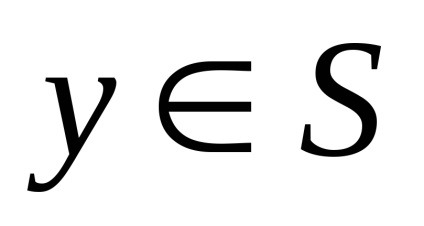



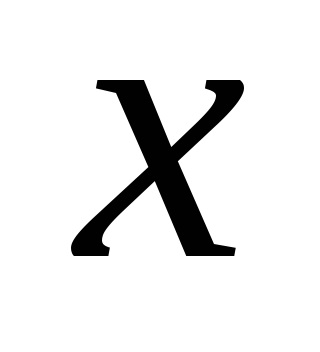
Exemple de seturi convexe
2. vidă.
3. Setul format din un singur punct
,
,
unde
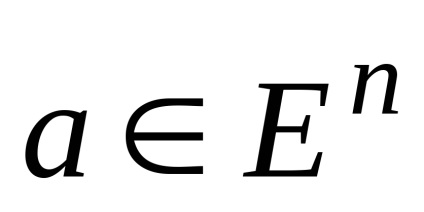
,
unde
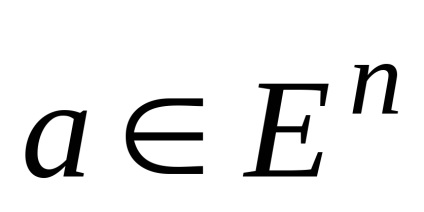
,
și y (k) - vectori definiți
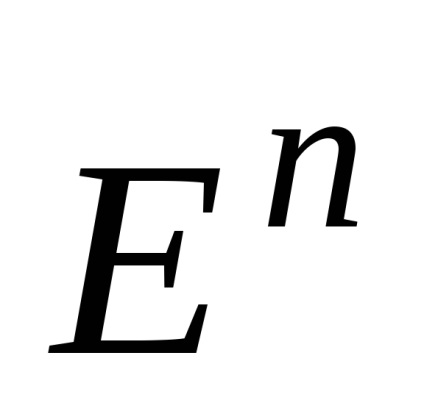
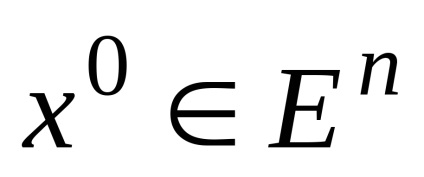
7. convexă Combinația (cochilie) dintr-un număr finit de puncte
.
Un astfel de set de geometrically reprezintă politopii convex n-dimensional.
8. Intersecția unui număr finit de jumătate
,
în cazul în care. Acest set se numește un set convexă poliedrică. În cazul în care aceasta este limitată, ea este, de asemenea, un poliedru convex. Astfel, există două reprezentări posibile ale unui poliedru convex - sub forma cocii convexe a unui set finit de puncte și un număr finit de intersecție jumătăților spațiilor definite de inegalitățile.
9. Ball rază r ≥0 centrat la
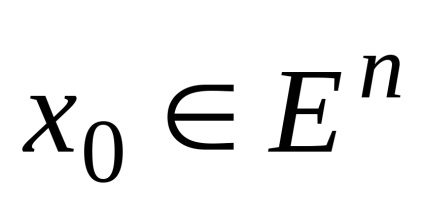
.
Ca exemple pot fi menționate de non-convexe stabilește o pluralitate de întregi sau setul de numere raționale.
2.1.2. Proprietățile seturilor convexe
Intersecția orice număr de seturi de convexe este un set convexă.
Unirea a două seturi convexe nu este neapărat convexă.
Exemplu: unirea a două puncte este un set convexă.
suma geometrică
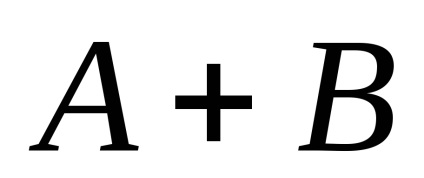
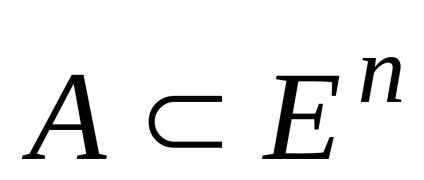
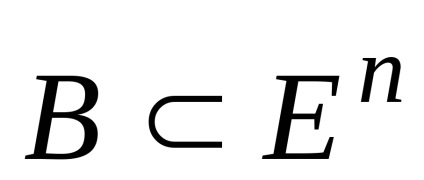
,
De asemenea, este convexă.
Artwork set convexe
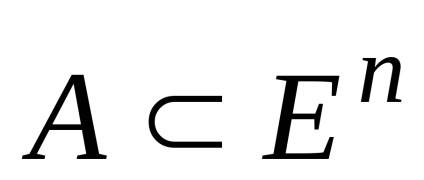
De asemenea, este convexă.
Aceste declarații rezultă din definiția unui set convexe. Să ne dovedesc, de exemplu, prima declarație la intersecția a două seturi
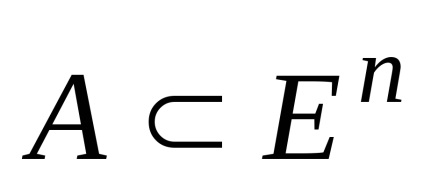
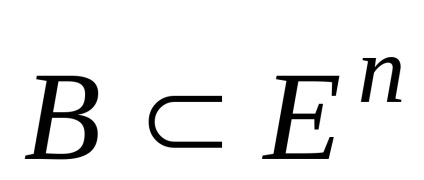
.
Convexitatea A și b obține că
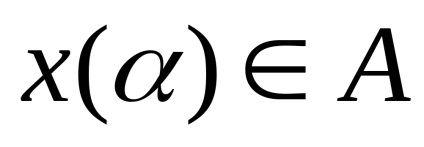
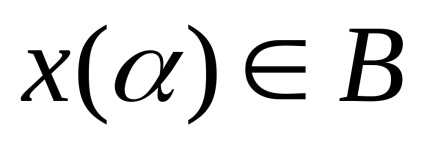
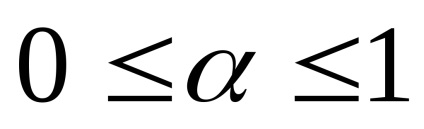
Determinarea .Krayney (extremale) punct al unui set convex astfel este numit un punct care nu poate fi reprezentat ca o combinație convexă a două puncte diferite ale acestui set.
Ca un exemplu, un poliedru convex. Punctele sale extreme sunt nodurile.
Definiția. MnozhestvoS
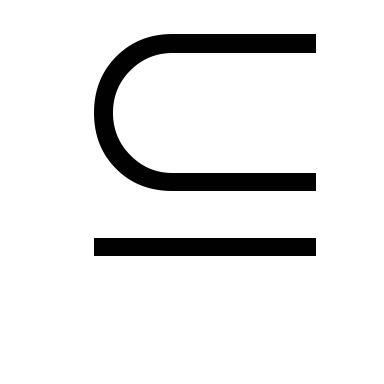
Un exemplu de un set strict convexă este închisă mingii.
2.1.3. hiperplan de sprijin
Luați în considerare cel mai important concept al hiperplan de sprijin. În primul rând, observăm că orice hiperplan. unde
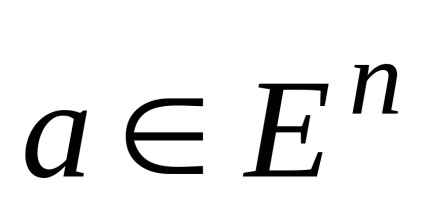
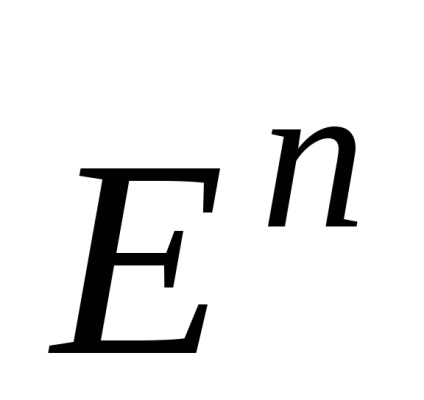
Hiperplan este intersecția acestor jumătăți de spații, în timp ce limita fiecăreia dintre ele.
Să presupunem că există un set convexă S și tochkay sale limită.
Definiția. GiperploskostH. care trece prin tochkuy și conține toate punctele într-unul din mnozhestvoS definite de închis-o jumătate este numit un hiperplan de sprijin pentru mnozhestvuS în tochkey.
Se poate demonstra că hiperplanul de suport se poate face prin orice punct de delimitare a unui set convexe. Ilustrarea hiperplan de susținere este prezentată în Fig. 3.1.
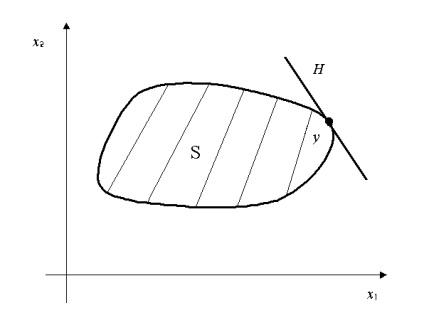
Fig. 3.1. Referință hiperplan H la un set convex S la punctul y.
Rețineți că hiperplan de sprijin poate să nu fie unic (vezi. Fig. 3.2).
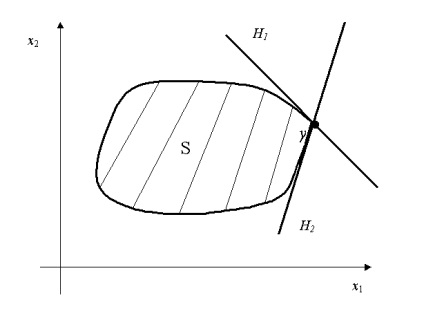
Fig. 3.2. Două referință hiperplan H1 și H2 la un set convex S la punctul y.
Să presupunem acum că două seturi nevidă A și b. GiperploskostH nazyvaetsyarazdelyayuschey hiperplan, în cazul în care toate punctele mnozhestvaA se află într-una dintre cele mai închise semi-spațiile definite de giperploskostyuH. și toate punctele mnozhestvaB se află într-o altă jumătate închisă definită. Se poate dovedi mai multe teoreme pe hiperplan de separare. Luați în considerare cele mai simple dintre ele. lăsa

Teorema 3.1. Pusta și b - două non-gol convexe set prichemØ. Apoi, acolo giperploskostH. separare mnozhestvaA iB.1
Exemple de hiperplane de separare sunt prezentate în Fig. 3.3 și 3.4.
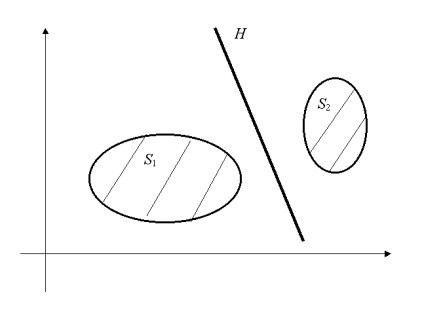
Fig. 3.3. H hiperplan separă seturile S1 și S2. nu au un punct comun
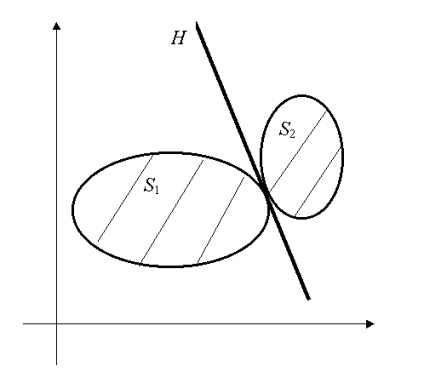
Fig. 3.4. H hiperplan separă seturile S1 și S2. cu un punct comun
Convex și funcții concave