Număr Curs 11, „Aplicații ale derivatului la funcția de anchetă“
O variabilă numită monotonă dacă aceasta se datorează modificărilor într-o singură direcție, adică, sau numai vozras-topire, sau doar scade. Evident, mișcarea unui punct x în direcția pozitivă a axei x este monoton crescătoare, iar în direcția opusă - monoton descrescătoare.
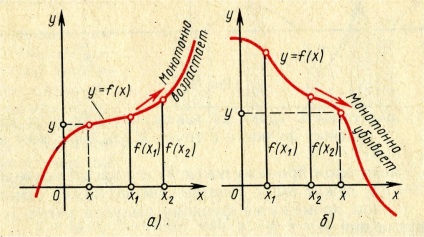
Fig. 3. Diagramele creșterea și descreșterea monoton monoton funcția.
Firește, intervalul (a, b) Să presupunem-Gaeta luat din domeniul funcției.
Un criteriu suficient pentru creșterea funcției (descreștere). Dacă funcția y = f (x) în intervalul diferențiabilă
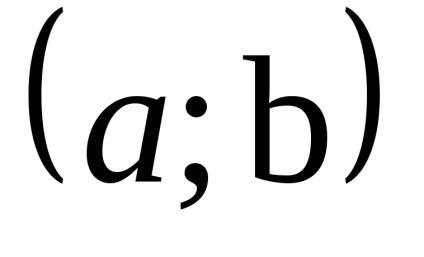
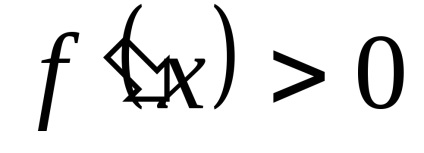
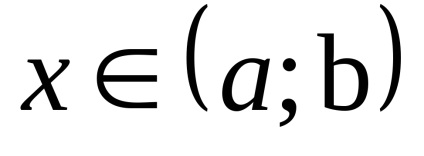
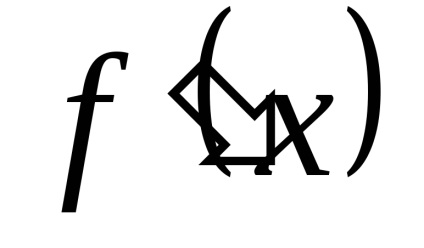
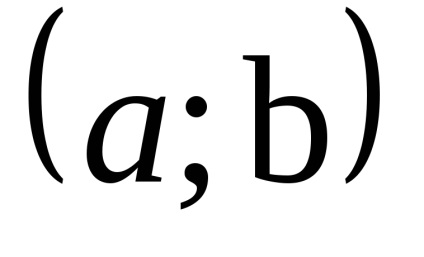
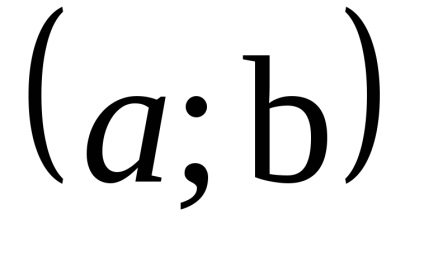
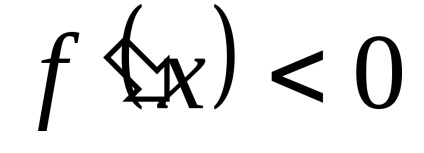
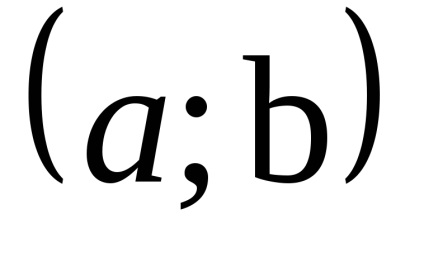
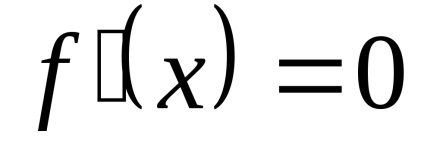
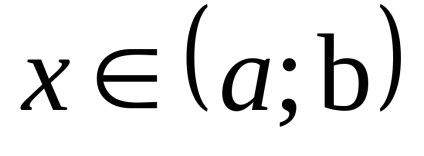
Se spune că funcția y = f (x) are un minim local la punctul h0є [a, b]. în cazul în care există o vecinătate a lui x0, conținută în întregime în [a, b] astfel încât pentru orice x. Acesta este deținută de primul din acest cartier, inegalitatea f (x)> f (x0).
Un criteriu suficient pentru funcțiile extreme. Punctul critic (domeniul intern punct al funcției, în care derivatul acestei funcții este zero sau nu există) este o funcție extremum. în cazul în care, în vecinătatea acestui punct al semnului modificări derivate, și punctul maxim. în cazul în care modificările derivate semn de la „+“ la „-“, și un punct minim. în cazul în care modificările derivate semn de la „-“ la „+“.
Cel mai mare (mai mică), valoarea funcției continue y = f (x) pe [a, b] realizată fie într-unul dintre punctele critice, sau într-unul din punctele de delimitare ale segmentului.
Se spune că funcția y = f (x) este convex în sus la x0. în cazul în care există o vecinătate a punctului x0 este astfel încât pentru toate punctele x tangentă la graficul funcției în punctul M0 (x0. y0) se află deasupra graficului (Fig. 4a). Se spune că funcția y = f (x) este convex la x0. în cazul în care există o vecinătate a punctului x0 este astfel încât pentru toate punctele x tangentă la graficul functiei punct M0 (x0, y0) se află sub grafic (Figura 4b.).
Dacă la un anumit interval (a, b) tangente la toate funcțiile GRA-fiku y = f (x) se află mai sus (sau mai jos) a graficului, apoi, la un anumit interval de timp este convexă în sus (sau în jos convexă).
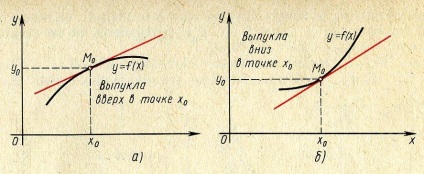
Fig. 4. Funcția convexe Grafice
Determinarea intervalelor punctelor convexitate și inflexiune
O condiție suficientă pentru convexitatea funcției pe intervalul. Dacă al doilea derivat f „(x) există în intervalul (a, b) și modificările semn în acest interval de timp, atunci:
1) f „(x)> 0 (+ semnul), funcția f (x) este convexă în jos într-un inter-ax (a, b);
2) când f „(x) <0 (знак - ) функция f(х) выпукла вверх на интервале (а;b).
Astfel, pentru a găsi intervale de concavitate și funcția convexitate în jos pentru a găsi al doilea pro-apos și rezolva inegalitatea f „(x) <0 и f"(х)> 0.
M0 (x0; f (x0)) a graficului y = f (x) on-se numește punct de inflexiune a acestui grafic, în cazul în care există-kai acolo cartier de x0, în care graficul funcției y = f (x) la stânga și în dreapta t. M0 are diferite direcții pe care-convexitate.
Fig. 5 prezintă o diagramă a unei funcții care are o inflexiune în punctul M0 (x0; f (x0)).
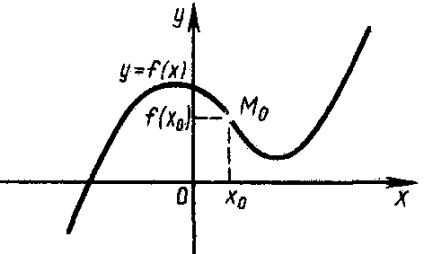
Fig. 5. Program de o funcție care are o inflexiune
Condiția necesară pentru existența punctului de inflexiune. Dacă funcția de la punctul x0 are un cot, apoi derivata a doua, în acest moment, fie nu există sau este zero.
Punctele la care derivata a doua este zero sau nu există, se numește punctele critice ale tipului II-lea. La aceste puncte de inflexiune sau nu poate fi. Această chestiune re-cutele cu următoarea etichetă.
Un criteriu suficient pentru existența unui punct de inflexiune. Să presupunem că funcția este definită și continuă într-un cartier de X0. inclusiv foarte punct. Să presupunem în continuare că al doilea Nye derivat de la acest punct este egal cu zero sau nu există. Apoi, dacă f „(x) <0 при х <х0 и f"(х)> 0 pentru x> x0 sau f „(x)> 0 pentru x <х0 и f"(х) <0 при х> x0. apoi M0 (x0. (f (x0)) este un punct de inflexiune y = f (x).
Mostre funcții de cercetare
Continuitate. Asimptotă. Deoarece funcția
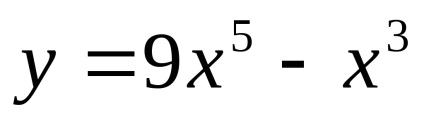

Paritatea. Deoarece domeniul funcției este simetrică în raport cu zero, vom afla dacă următoarele egalități:
. În consecință, funcția este impară. Graficul său este simetric față de origine.
Funcția nu este periodică.
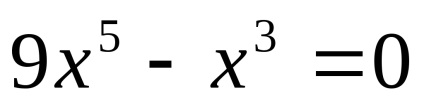
(0; 0);
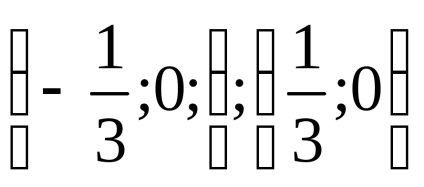
funcție monotonă. Extremele funcțiilor.
2) continuitate. Asimptotă. Această funcție este definită pentru toate valorile
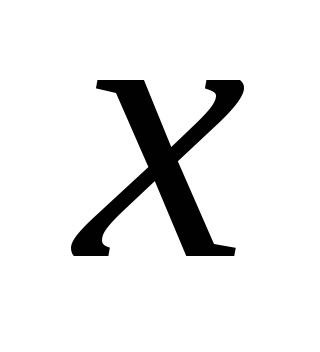
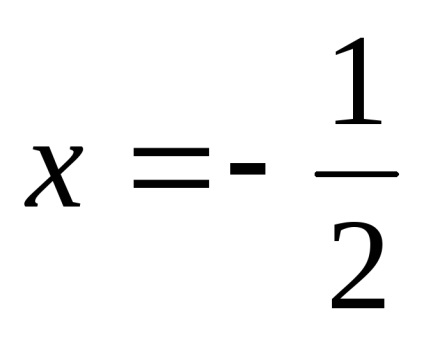
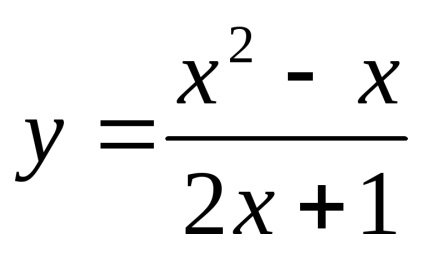
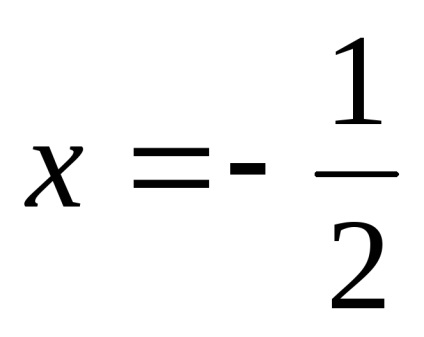
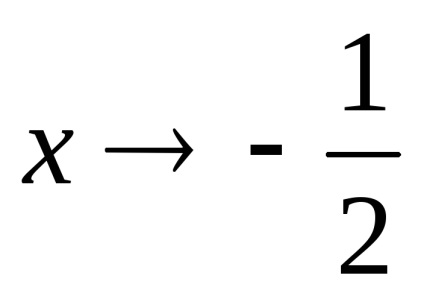
.
.
În consecință, funcția
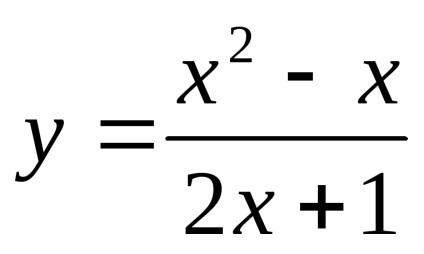
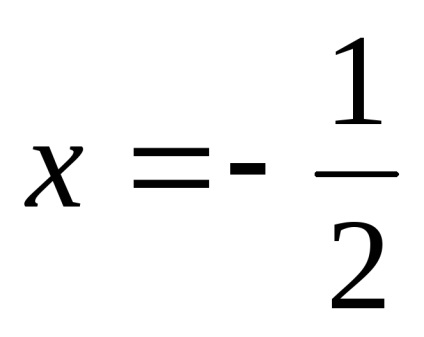
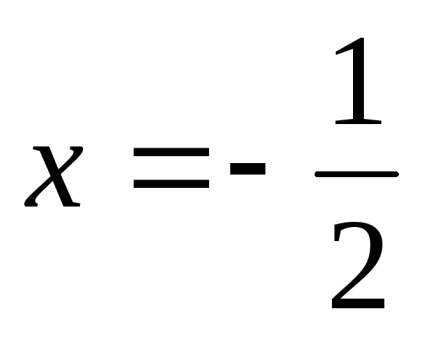
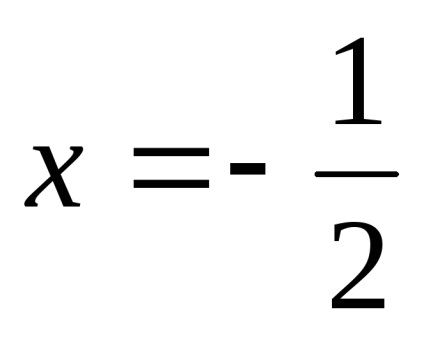
Găsim panta asimptota.
Astfel,
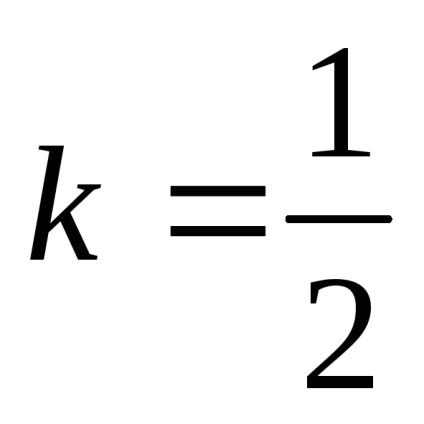
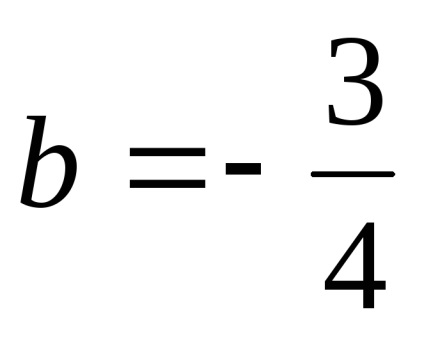
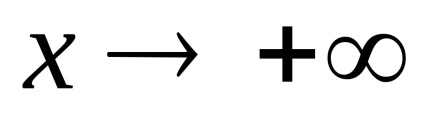
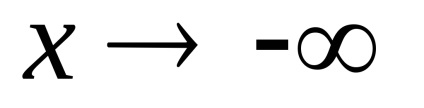
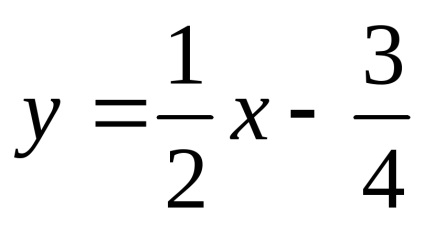
3) Paritatea. Domeniul de definiție nu este simetrică în raport cu zero, deci funcția nu este nici măcar, nici ciudat. forma generală a funcției.
4) Funcția nu este periodică.
5) zerouri. y = 0. dacă x 2 -x = 0; x (x-1) = 0; x1 = x2 = 0 sau 1
(0, 0), (1, 0) - graficul punctelor de intersecție cu axele de coordonate.
6) monotonie. Puncte extremelor.