Definiția. Etapa se va numi o matrice, care are următoarele proprietăți:
1) dacă rândul i-lea este zero, atunci (I + 1) th rând este de asemenea zero
2) în cazul în care primele elemente nenule ale i-lea și (I + 1) rânduri sunt aranjate în -lea coloanele cu indicii k și R, respectiv, k Condiții 2) prevede majorarea zerouri obligatorii rămase în tranziția de la rândul i-lea la (I + 1) Rândul -lea. De exemplu, matricea este în trepte, iar matricea nu sunt decalate. Teorema 5.1. Orice matrice poate duce la trepte de rânduri ale matricei de transformare elementare. Să ilustrăm această teoremă printr-un exemplu. Matricea rezultată # 9472; viteză. Definiția. Rangul unei matrice să fie numărul de rânduri nenule sub forma în trepte a matricei. De exemplu, gradul de matricei A din exemplul anterior este 3. Determinanii și proprietățile lor. matrice Inverse și calcul. Identificatorul secundar. Să considerăm matricea pătrată a doua comandă Definiția. al doilea factor determinant, pentru matricea A corespunzătoare este un număr calculat prin formula Elementele AIJ sunt numite elemente ale determinant # 9474, # 9474 A;, elemente A11. a22 formează principalul diagonală. și elementele A12. A21 # 9472; accidentale. Exemplu.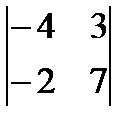
Determinanții al treilea ordin.
Să considerăm matricea pătrată a treilea ordin
Definiția. Determinantul treilea ordin, matricea corespunzătoare este un număr calculat prin formula
Pentru a aminti care funcționează pe partea dreaptă ar trebui să fie luate cu un „plus“ și care # 9472; cu semnul „minus“, este util să ne amintim regula, care se numește regula triunghi.
1)
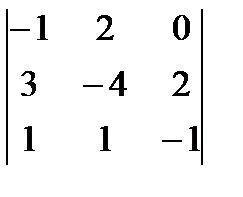
2)
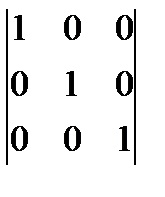
Luați în considerare un alt mod de a calcula determinant al treilea ordin.
Definiția. Minor determinant elementul aij este determinant obtinut din aceasta cu anularea i-lea rand si coloana j-lea. Cofactor de AIJ elementului determinant Aij este numit minor Mij său. luate cu semnul (-1) i + j.
Exemplu. Calculăm M23 Minor și cofactor A23 A23 element din matricea
Calculăm Minor M23:
M23 =
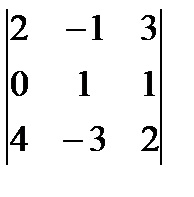
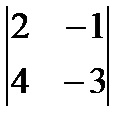
TEOREMA 1. Factorul determinant este suma a treia produselor de comandă ale elementelor unui rând (coloană) prin cofactori lor.
Dovada. prin definiție,
Să ne alege, de exemplu, al doilea rând și pentru a găsi cofactor A21. A22. A23: