Pe măsură ce sistemul în cauză în teorema poate fi orice sistem mecanic format din oricare dintre organismele.
Cantitatea de mișcare (impuls) a sistemului mecanic menționat valoarea egală cu suma valorilor de mișcare (impulsuri) toate corpurile din sistem. Impulsul forțelor exterioare care acționează asupra sistemului corpului - este suma tuturor momentelor forțelor exterioare care acționează asupra sistemului corpului.
Teorema privind modificarea cantității de mișcare a creanțelor
Schimbarea cantității de mișcare a sistemului pentru o perioadă de timp egală cu impulsul de forțe externe care acționează asupra sistemului, pentru aceeași perioadă de timp.
Legea conservării mișcării sistemului
Dacă suma tuturor forțelor exterioare care acționează asupra sistemului este zero, atunci cantitatea de mișcare (impuls) a sistemului este constantă.
Introducem schimbarea impulsul de forțe externe, obținem o expresie a teoremei privind modificarea numărului în formă de mișcare diferențială a sistemului:
Astfel, fiecare dintre ultimele ecuații obținute sugerează: schimbarea cantității de mișcare a sistemului are loc numai prin acțiunea forțelor externe și a forțelor interne nu au nici un efect asupra acestei valori nu se poate face.
Integrarea ambele părți ale acestei ecuații în raport cu un interval de timp arbitrar ales între unele și să obțină o expresie a teoremei privind modificarea numărului de mișcare a sistemului în formă integrală:
in care valorile lui u în cantitatea de mișcare a momentelor vremeniisootvetstvenno, un- pulsul forțelor externe în timpul intervalului de timp. În conformitate cu acest lucru și notația introduse anterior efectuate
Legea conservării impulsului (legea conservării impulsului) prevede că sistemul de telefonie vector summaimpulsovvseh este constantă, în cazul în care suma vectorială a forțelor exterioare care acționează asupra sistemului este zero.
(impuls unghiulara kg · m 2 · s -1)
Teorema de schimbare a momentului cinetic în raport cu centrul
derivata a momentului cinetic (momentul cinetic) cu privire la un punct material al unui punct central fix forțe egale care acționează asupra punctului în raport cu același centru.
Teorema de schimbare a momentului cinetic în raport cu axa
derivata a momentului cinetic (momentul cinetic) al unui punct material în raport cu o anumită axă fixă egală cu momentul care acționează asupra acestui punct de forță în jurul aceleiași axe.
Luați în considerare materialul massoym punctul M. se deplasează sub acțiunea silyF (Figura 3.1). Noi scrie vectorul construct și momentul unghiular (momentul cinetic) M0 punctului material relativ tsentraO:
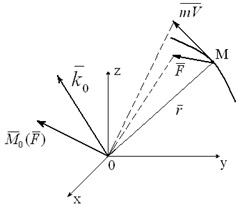
Diferențierea momentului cinetic (momentului cinetic K0) Timpul:
Ecuația (3.4) exprimă teorema de schimbare a momentului cinetic (momentul cinetic) a unui punct în raport material centrul: derivata momentului unghiular (impuls unghiular) al unui punct în raport de material într-o oarecare centru fix egal cu momentul în care acționează pe punctul de forță în raport cu același centru.
Proiectarea ecuația (3.4) pe axa coordonatelor carteziene, obținem
Egalitatea (3.5) exprimă teorema schimbării momentului cinetic (moment unghiular) al unui punct în raport material axa: derivata a momentului cinetic (momentul cinetic) al unui punct material în raport cu o axă fixă este egală cu momentul acțiunii în acest moment o forță în jurul aceleiași axe .
Considerăm implicațiile teoremelor (3.4) și (3.5).
Corolarul 1. Se consideră cazul în care silaF pe tot parcursul mișcării trece prin punctul fix tsentrO (forță centrală caz), adică kogdaM0 (F) = 0. Atunci Teorema (3.4) chtok0 = const,
și anume în cazul momentului central de forță unghiular (moment unghiular) relativului material punctul central al acestei forțe rămâne constantă în mărime și direcție (figura 3.2).
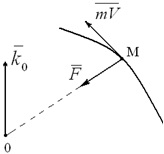
De la starea K0 = const implică faptul că traiectoria punctului în mișcare este o curbă plan, a cărui plan trece prin centrul acestei forțe.
și anume în cazul în care momentul de forță care acționează asupra punctului în raport cu o axă fixă este întotdeauna zero, impulsul unghiular (momentul cinetic) al punctului în raport cu această axă rămâne constantă.
Dovada teoremei Ob ihmenenii impuls
Să sistemul format din tocheks materiale Massamá accelerații. Toate forțele care acționează asupra sistemului corpului, împărțit în două tipuri:
forțe externe - forțele care acționează pe partea organelor în afara sistemului în cauză. Rezultanta forțelor exterioare care acționează asupra unui număr punct material i este notat.
Forțele interne - forțe care interacționează unele cu altele a corpului sistemului. Forța cu care un punct cu indicele i operează cu nomeromk punct. vom nota, și forța vozdeystviyai punct-lea NAK-lea punct -. Este evident că, dacă, atunci
Folosind notațiile introduse, scrie legea a doua a lui Newton la fiecare dintre punctele de materiale considerate ca fiind
Având în vedere că și însumarea toate ecuațiile de a doua legea lui Newton, obținem:
Expresia este suma tuturor forțelor interne care acționează asupra sistemului. Potrivit lui Newton a treia lege în suma fiecărei silatakaya silesootvetstvuet, chtoi, apoi vypolnyaetsyaPoskolku întreaga cantitate este format din astfel de perechi, iar suma în sine este zero. Astfel, putem scrie
Utilizarea sistemului pentru suma de notație de circulație, obținem
Introducem schimbarea impulsul de forțe externe, obținem o expresie a teoremei privind modificarea numărului în formă de mișcare diferențială a sistemului:
Astfel, fiecare dintre ultimele ecuații obținute sugerează: schimbarea cantității de mișcare a sistemului are loc numai prin acțiunea forțelor externe și a forțelor interne nu au nici un efect asupra acestei valori nu se poate face.
Integrarea ambele părți ale acestei ecuații în raport cu un interval de timp arbitrar ales între unele și să obțină o expresie a teoremei privind modificarea numărului de mișcare a sistemului în formă integrală:
in care valorile lui u în cantitatea de mișcare a momentelor vremeniisootvetstvenno, un- pulsul forțelor externe în timpul intervalului de timp. În conformitate cu acest lucru și notația introduse anterior efectuate