Capitolul 7 Elemente speciale (private) teoria relativității
În cazul în care un cadru de referință se deplasează în raport cu celălalt și în mod uniform într-o linie dreaptă și într-una dintre ele sunt adevărate legi ale dinamicii newtoniene, aceste sisteme sunt inerțiale. De asemenea, sa constatat că, în toate sistemele de referință inerțiale legile dinamicii clasice au aceeași formă; Acest principiu sutmehanicheskogo relativității (principiul relativității galilean).
Pentru a demonstra acest lucru, să considerăm două cadre de referință: sistem inerțial K (cu coordonatele x, y, z), care se presupune în mod convențional fi fixat, iar sistemul K „(cu coordonatele x“, y „z“), care se deplasează în raport cu rectilinie uniformă la o viteză (= const). Numărătoarea inversă va începe din momentul în care originea celor două sisteme coincid. Să presupunem că la un moment t aranjament arbitrar al acestor sisteme relativ una față de cealaltă a forma prezentată în ris.58. Viteza este direcționată de-a lungul 00 „vectorul raza de la O la O“.
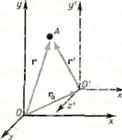
Găsim relația dintre coordonatele unui punct arbitrar A pe ambele sisteme. De la ris.58 văzut că
Ecuația (34.1) pot fi scrise în proiecții pe axele de coordonate:
Ecuațiile (34.1) și (34.2) sunt numite Galileanului transformări de coordonate.
În cazul special în care se mișcă K „cu o viteză pe direcția pozitivă a axei x sistemului K. (la axele de timp inițiale coincid), transformarea coordonatelor Galileo au forma
În mecanica clasică, se presupune că trecerea timpului nu depinde de mișcarea relativă a sistemelor de referință, adică, la transformarea (34,2), puteți adăuga încă o ecuație ..:
Relații înregistrate sunt valabile numai în cazul mecanicii clasice (), și la viteze comparabile cu viteza luminii, transformarea Galileo înlocuiește cu transformări mai generale Lorentz (H.Lorents (1853-1928) - fizician olandez) (§36).
Diferențierea expresia (34.1) timp pe bază (luând în considerare (34,3)), obținem ecuația
care reprezintă viteza de plus soboypravilo la mecanica clasică.
Accelerația în cadru de referință K
Astfel, accelerația punctului A în cadrele de referință K și K“, se deplasează în raport cu celălalt în mod uniform și rectiliniu aceeași:
Prin urmare, în cazul în care punctul A de pe un alt organism nu este valid (= 0), în conformitate cu (34.5), n = 0, m. E. System R „este un inerțial (punct se deplasează în raport cu acesta în mod uniform și rectiliniu sau în repaus).
Astfel, din ecuația (34.5) urmează principiul mecanic dovada relativității: ecuația dinamicii la trecerea de la un sistem de referință inerțial la altul nu sunt modificate, adică yavlyayutsyainvariantnymi față de transformări de coordonate ... Galileo a menționat că orice experimente mecanice, efectuate în cadrul inerțial de referință, este imposibil să se stabilească dacă este în repaus sau se deplasează uniform într-o linie dreaptă. De exemplu, stând în cabina navei, se deplasează uniform într-o linie dreaptă, nu putem determina nava este în repaus sau în mișcare, nu uită pe fereastră.