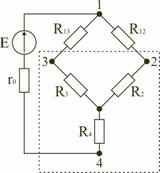
Parametrul r al elementului de rezistență în conformitate cu legea lui Ohm definește relația dintre valorile instantanee ale tensiunii și curentului u = ri. Rezistența elementului rezistiv r în circuitele de curent alternativ numit rezistență activă. Rezistența elementului rezistiv este o funcție de frecvență, curentul care curge prin ea, și poate crește odată cu creșterea frecvenței datorită manifestării efectului de crowding curent. Elementul rezistiv. Lăsați tensiunea pe elementul rezistiv cu rezistență R (fig. 4.1a, b) sinusoidal, adică u (t) = Um Sin (# 969; t + # 968; u) Deoarece tensiunea instantanee și valorile curente pentru elementul rezistiv sunt conectate prin legea lui Ohm, I (t) = u (t) / R = (Um / R) Sin ( # 969; t + # 968; u) sau i (t) = Im Sin (# 969; t + # 968; i), unde Im = Um / R .Mgnovennaya putere la elementul rezistiv este definit de p (t) = u (t ) i (t) = UI- UICos2 # 969; t = p = + p
Puterea variază de la zero la un maxim, luând doar valori pozitive. Acest lucru înseamnă că, pentru orice direcție a curentului furnizat de la sursa de energie la elementul rezistiv și se disipă sub formă de căldură. Perioada medie a puterii AC (sau activ) este P = p == UI = I2R = U2g, Wat. ca # 966; = 0, atunci puterea reactivă este 0, adică, Q = UISin # 966; = 0.
Putere maximă este egală cu puterea activă, adică, S = UI.
rezistența elementului de rezistență în forma consecință: a) impedanța complexă a elementului rezistiv cuprinde numai componenta activă (componenta reactivă este egală cu zero), adică b) impedanța rezistivă elementului z = R; c) argumentul impedanței complex este 0 (# 966 = 0) și, prin urmare, vectorii de tensiune elementul rezistiv și un curent în ea aceeași direcție (Figura 4.1 in) .. Conductivitatea complexă a elementului rezistiv este inversul impedanței complexe, adică YR = 1 / ZR = (1 / R) ej0 = 1 / R, A se vedea. Să curent elementul inductiv în elementul inductiv cu o inductanță L (fig. 4.2a, b) este sinusoidală, adică i (t) = Im Sin ( # 969; t + # 968; i). Deoarece valorile instantanee ale tensiunii de pe un element inductiv proporțional cu rata de variație a curentului, atunci u (t) = L i.d. / dt = Im # 969; L Cos (# 969; t + # 968; i) = Im # 969; L Sin # 969; t + # 968; i + π / 2), sau u (t) = UmSin (# 969; t + # 968; u), în cazul în care Um = Im # 969; L este amplitudinea tensiunii și # 968; u = # 968; i + π / 2 tensiune de fază inițială.
xL = # 969; L, Ohm numit reactanța inductivă.
Amploarea bL, reactanța inductivă inversă se numește conductivitate inductiv bL = 1 / xL = 1 / # 969; L, Sim. După cum se poate observa, la o tensiune de amplitudine constantă pe un element inductiv cu frecvență proporțională scade amplitudinea curentului. Defazajul între tensiune și curent la toate frecvențele rămâne constantă și egală cu tt / 2. Puterea instantanee în elementul inductiv este definit de p (t) = u (t) i (t) = UISin2 (# 969; t) = p
variabilă de alimentare conține doar componenta sinusoidală, variind de la de două ori frecvența. La intervale de o perioadă în care tensiunea și semnele actuale sunt la fel, energia este furnizată inductanța de stocarea sursă în bobina de câmp magnetic. La intervale de o perioadă în care tensiunea și curentul sunt semne diferite, energia stocată în elementul inductiv este returnat înapoi la sursa. Perioada medie a AC (sau activă) puterea elementului inductiv este zero, adică P = UICos (π / 2) = 0.
ca # 966; = Π / 2, atunci puterea reactivă este pozitivă și este egală cu Q = UISin # 966; = UI. Putere maximă este egală în mărime de putere reactivă, adică S = UI. Identificând raportul dintre amplitudinea integrate de tensiune la amplitudinea actuală a complexului. Obținem o expresie pentru impedanța complexă a elementului inductiv sub forma Deoarece valoarea instantanee a curentului într-un element capacitiv în mod proporțional cu rata de schimbare tensiunii de alimentare, i (t) = C du / dt = Um # 969; C Cos (# 969; t + # 968; u) = Um # 969; C Sin (# 969; t + # 968; u + π / 2) sau i (t) = Im Sin (# 969; t + # 968; i), unde Im = Um # 969 C, iar amplitudinea curentului # 968; i = # 968; u + π / 2 faze de curent inițial. Bc valoare, reactanța capacitivă invers se numește conductivitate capacitiv. bc = 1 / xc = # 969; C, Sim După cum se poate observa, la o amplitudine constantă de tensiune de la un element capacitiv cu frecvență proporțională cu curentul crește amplitudinea. Defazajul între tensiune și curent la toate frecvențele rămâne constantă și egală cu - π / 2. Puterea instantanee într-un element capacitiv definit prin formulele p (t) = u (t) i (t) = UISin2 (# 969; t + # 968; u) = p
Perioada medie a CA (sau activă) alimentarea cu energie a elementului capacitiv este egal cu zero, adică P = UICos (-π / 2) = 0. ca # 966; = - π / 2, atunci puterea reactivă este negativă și este egală cu Q = UISin # 966; = -UI.
Puterea totală egală în mărime a puterii reactive, adică S = UI. Prin găsirea raportului de amplitudine complexă a tensiunii la amplitudinea complexă a curentului, obținem o expresie pentru impedanța complexă a elementului capacitiv în sus
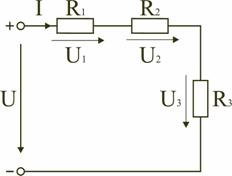
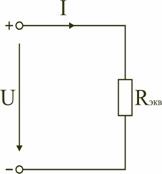
Legea lui Ohm 6. pentru subcircuit intensitatea curentului într-un conductor este proporțională cu tensiunea de la capetele sale și invers proporțional cu rezistența conductorului:
Orice circuit electric poate fi caracterizat amperaj, tensiune și rezistență.
legea lui Ohm pentru lanțul complet - curentul în circuitul proporțională cu curentul din circuit și înapoi EMF proporțională cu rezistențele de circuit sumă și rezistența sursă internă.
legiferată lui Ohm pentru lanțul complet este după cum urmează: curentul într-un circuit electric este direct proporțională cu tensiunea aplicată lanțului și invers proporțională cu suma rezistenței interne a sursei de alimentare și rezistența totală a lungul circuitului.
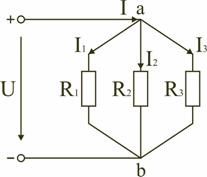
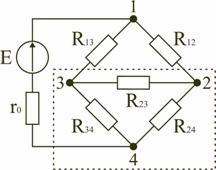
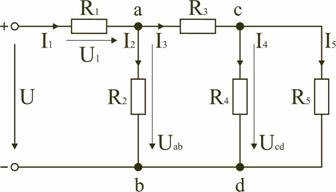
Într-un circuit punte de rezistență R13, R12, R23 și R24, R34, R23 conectat într-un "delta" circuit. Rezistența echivalentă a acestui circuit poate fi determinată numai după înlocuirea unuia dintre triunghiuri, de exemplu triunghi stea r24 R34 R23 R2 R3 R4 (fig. 1.13). Această înlocuire va fi echivalentă cu, în cazul în care nu determină o schimbare a curentului