coeficienți binom sunt valorile
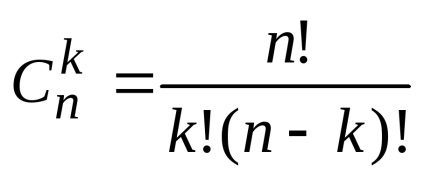
care exprimă numărul de combinații de n elemente de transport de tehnologie. Aceste valori au următoarele proprietăți.
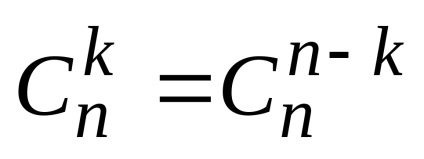
În formula binomului, acest lucru înseamnă că coeficienții, în picioare pe aceleași poziții de pe stânga și la dreapta capetele formulele sunt, de exemplu:
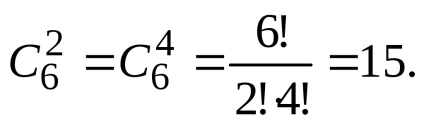
De fapt,
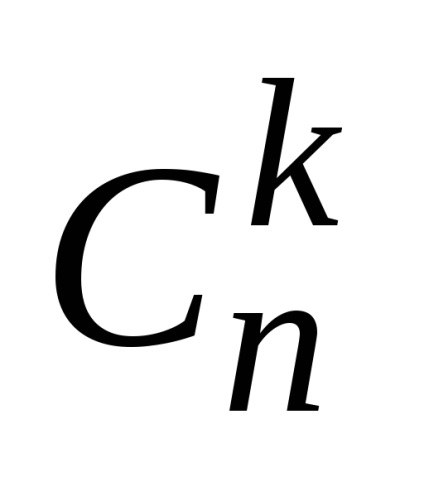
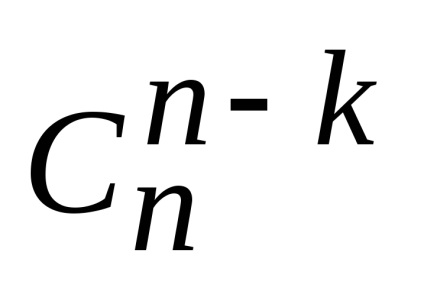
Să. număr
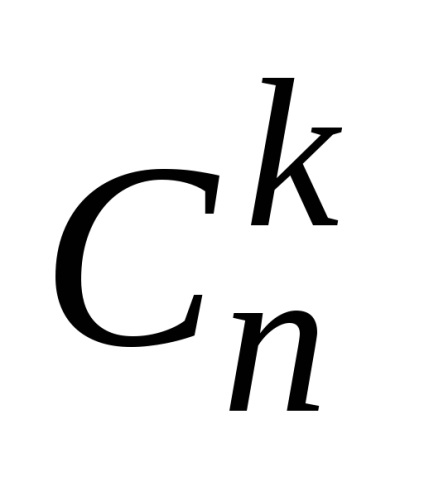
1) element al subgrupul care nu conține
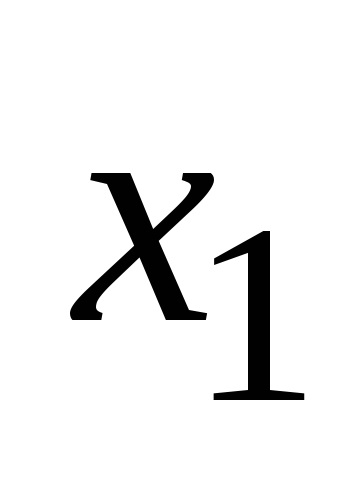
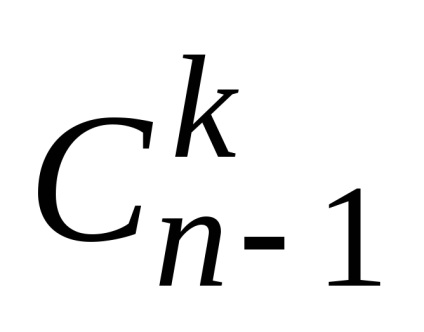
2) un element de subansamblu care conține
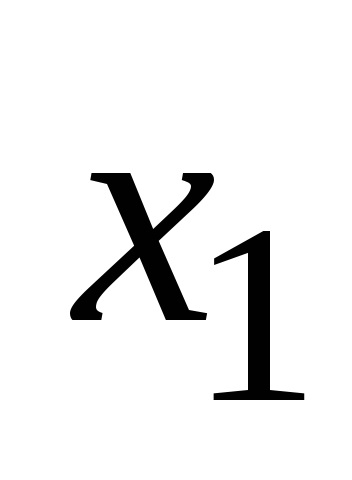
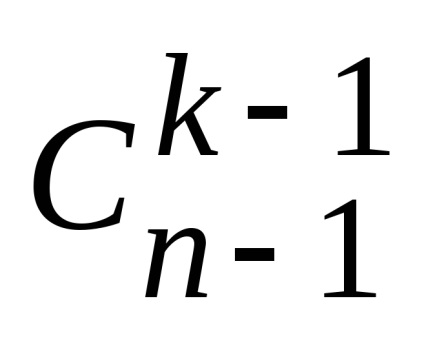
pentru că Aceste clase nu se intersectează, atunci regula însumează numărul tuturor subseturilor elementul k este egal cu mnozhestvaX
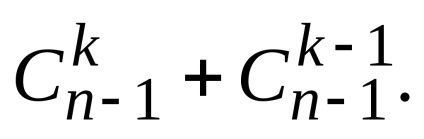
Pe baza acestei proprietăți construirea triunghiul lui Pascal (Fig. 2.2) în al n-lea rând, care sunt coeficienții dilatărilor binomială
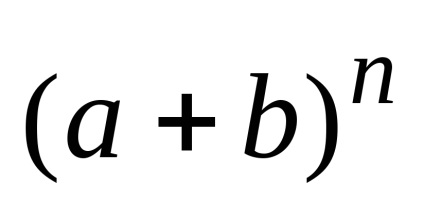
Înlocuind în Eq binom
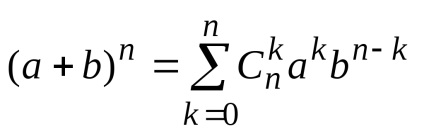
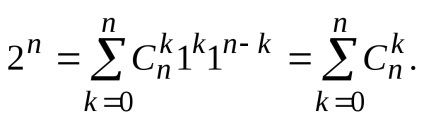
Rețineți că, în ceea ce privește teoria mulțimilor exprimă suma numărului de toate podmnozhestvn set -Element. Prin puterea teoremei booleene (a se vedea punctul. 1.4.4), numărul este
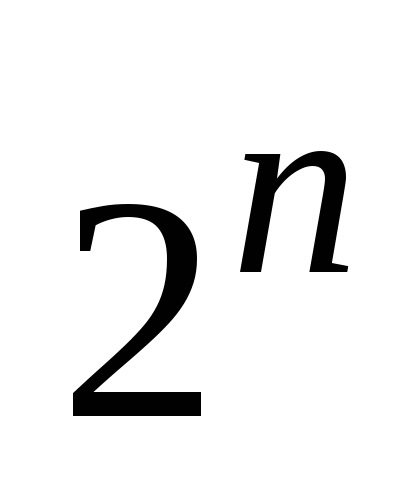
Amplasat în teorema binomială
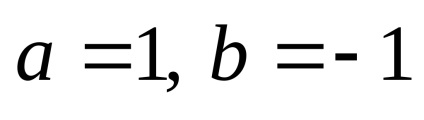
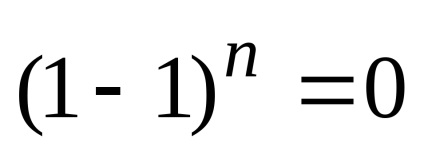
Această din urmă proprietate este convenabil să scrie, dacă toți coeficienții cu semne negative în partea din stânga a formulei:
atunci proprietatea este ușor de stocat în formulare verbală „suma coeficienților binomiali cu numere impare egal cu suma coeficienților binomiali cu numere chiar.“
Sarcină. Găsiți un membru al expansiunii binomială
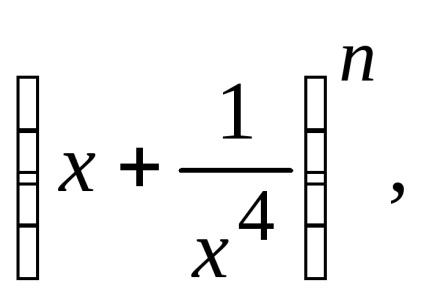
Decizie. Prin sumă diferență de proprietate coeficienții binomiali cu numere chiar și este, de asemenea, egal cu 512, atunci suma tuturor coeficienților egal cu 512 + 512 = 1024. Dar valoarea proprietății, acest număr este. prin urmare
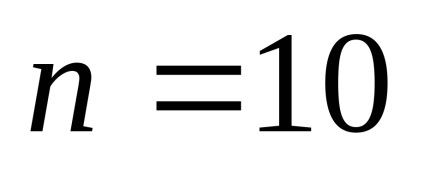
pe termen lung în expansiune
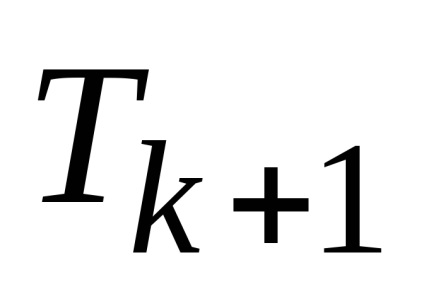

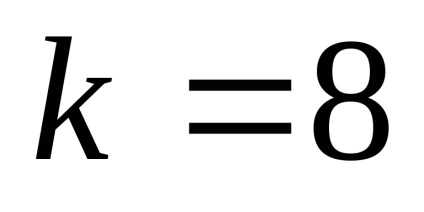
proprietate maximă. În cazul în care gradul de binoman - chiar, printre coeficienții binomiali au un maxim la
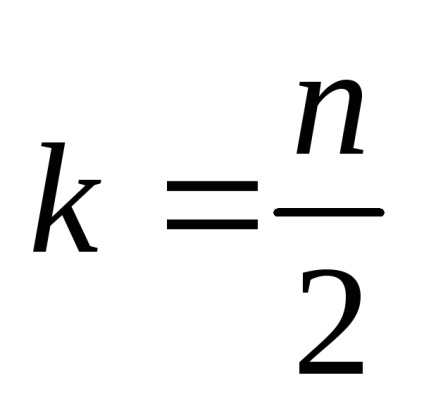
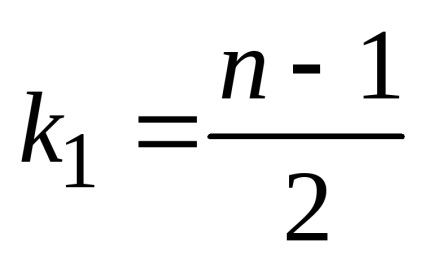
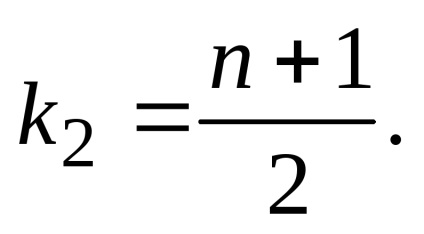
Astfel, atunci când
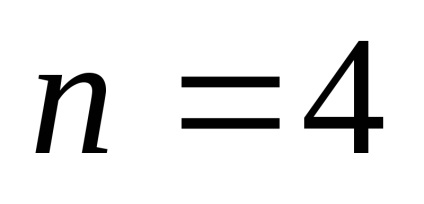
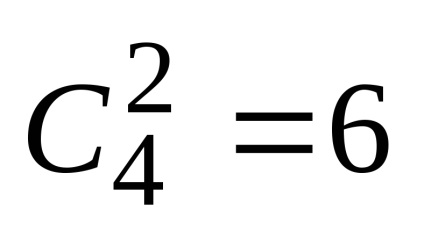
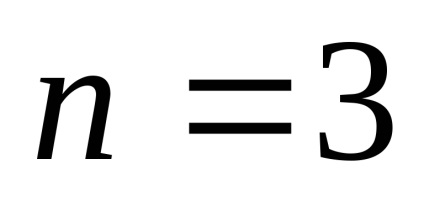
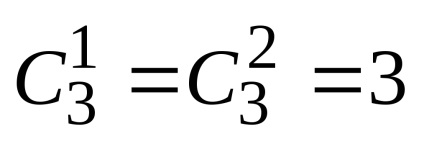
2.1.13. Calcule aproximative folosind binomului lui Newton
Amplasat în teorema binomială
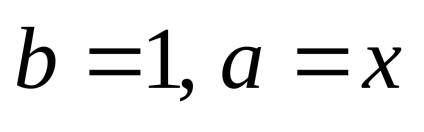
Această formulă este convenabil să se folosească pentru calcule aproximative pentru valori mici ale lui x (
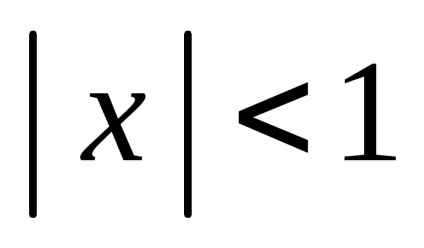
Exemplul 1. Folosind formula binomului lui Newton, compute
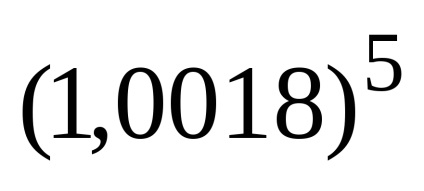
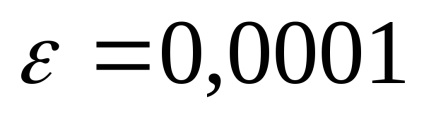
În conformitate cu formula de mai sus, avem:
Estimăm al treilea termen în această sumă.
termenii rămase mai puțin. Prin urmare, toți termenii din a treia pot fi eliminate. atunci
Exemplul 2. Se calculează
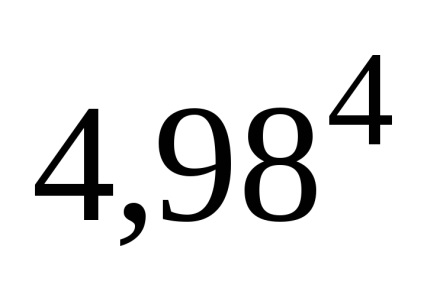
Estimăm al treilea termen:
.
Estimăm al patrulea termen:
Deci, toți termenii din al patrulea, pot fi eliminate. obținem