Poziția unei linii drepte în spațiu este complet determinat de oricare două dintre punctele sale. În general, proiecția unei linii drepte este o linie dreaptă, într-un caz particular - un punct, în cazul în care linia este perpendiculară pe planul de proiecție. Pentru a construi linia proeminențelor este suficient pentru a avea o proiecție a două puncte ale sale sau un punct de o proeminență a unei linii drepte și direcția în spațiu.
Conform poziției sale în spațiu în raport cu planurile de proiecție linii drepte sunt împărțite în poziție generală drepte, nivel, și proiecte.
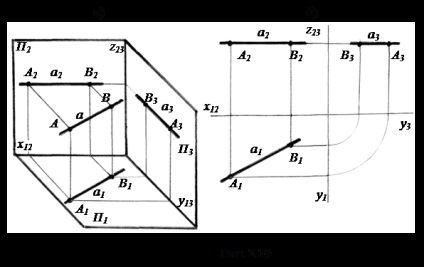
2.2.1. Poziția generală directă. Este direct, nu paralelă și nu perpendicular pe planul de proiecție. Proiecția A1 B1. A2 B2 A3 B3 și linia segmentului AB AB poziția generală (fig. 2.18, a) sunt înclinate în unghi ascuțit către axele x12. Y13 și Z23. Lungimea proiecției segmentului acestei linii este întotdeauna mai mică decât segmentul. Trehkartinny complex desen un segment de linie în poziție generală, construită pe două puncte A și B este prezentată în figura 2.18 b,.


3) profilul de nivel. Paralel A3 (direct cu FE segment cu ea în fig. 2.20, b). Fig. 2.20 linii de imagine vizuală b și c nu sunt prezentate în raport cu planul de proiecție.

Unghiurile de înclinare a nivelului un impact direct, b și c pentru avioanele P1 proiecții. P2 și P3, respectiv, pentru a indica # 945;. # 946; și # 947; (Fig. 2.19 unghiuri # 945;. # 946; și # 947; nu este prezentat).
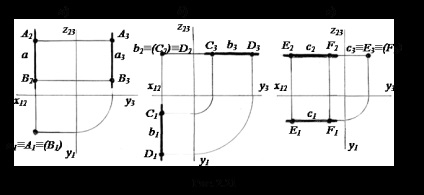
2.2.3. Proiectarea drept. Această linie dreaptă perpendicular pe una dintre planurile de proiecție și paralelă cu celelalte două. Prin urmare, avem trei tipuri de linii proeminente:
1) proeminente linie orizontal dreaptă perpendicular P1 (segment AB și de la aceasta la figura 2.21, a) .;
2)-frontală proeminentă o linie perpendiculară pe P2 (linia b cu segmentul CD pe ea în figura 2.21, b) .;
3) proeminente profil linie perpendiculară pe P3 (linia c cu segmentul EF pe ea în Fig. 2.21 in).
Fig. 2.21 între paranteze au proiecția punctelor invizibile. Problema determinării vizibilității punctelor asupra proiecțiilor vor fi luate în considerare în continuare mai jos în n. „Linii Skew“.
În proiectarea proiecția directă cu același nume este un punct care rezultă din natura liniei drepte proeminentă a lungul căreia este proiectată.
Fiecare proiecție oppositely proeminente perpendicular pe linia axei, care îl separă de numele proiecției, iar segmentul de proiecție a dispus opus la nivelul liniei este valoarea reală a acestui interval.

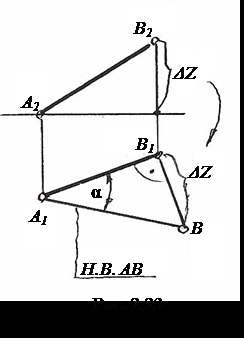
2.2.4. Determinarea dimensiunii reale a unui segment de linie în poziția generală. Full-size pozițiile linie privată poate fi determinată imediat pe desen complex această linie.

avion suplimentar # 928; 4 deținute parallelnoAB (x14 || A1 B1). AB direct transformat într-o poziție frontală, deci A4 B4 - dimensiunea reală a AB.
Având plan suplimentar # 928; 5 || AB (x25 || A2 B2) viață velichinuAB, poate fi de asemenea determinată. A5 B5 - velichinaAB naturale. Sistemul Direct AB 928 # 2 - # 928; 5 devenit orizontală.
2.2.5. Poziția relativă a liniilor. Liniile drepte în spațiu pot fi paralele, se suprapun și se încrucișa.
Linii paralele. Din proprietățile proiecții paralele, rezultă că în cazul în care liniile sunt paralele în spațiu, toate cele trei perechi de același nume proiecții paralele. Evident că poziția opusă: dacă același nume al liniilor de proiecție sunt paralele, atunci liniile sunt paralele în spațiu.
Pentru a defini linii paralele, în general, este suficient paralelismul dintre cele două perechi de proeminențe similare. Dacă paralelismul este determinată de liniile de nivel, una dintre cele două perechi de proeminențe paralele să fie proiecția pe același plan.

Intersectarea linii. Două linii intersectate se află în același plan și au un punct comun. Din proiecții paralele de proprietăți cunoscute, că în cazul în care punctul se află pe linia, proiecțiile sale se află pe o linie dreaptă proiecții. Dacă punctul se află pe linie și pe de altă parte, t. E. Pentru a direcționa punctul de intersecție, apoi proiecția sa trebuie să se întindă pe două linii drepte de proiecții similare și, în consecință, proiecțiile din punctul de intersecție al liniilor.
Astfel, în cazul în care segmentele AB și CD ale celor două linii se intersectează în proiecția punctului segmente K. A1 B1 C1 D1 și se intersectează în punctul K1. care este proiecția punctului K (figura. 2.26, a). Prin urmare, în cazul în care aceleași linii de proiecție nume se intersectează în punctele situate pe o singură linie de comunicare de proiecție, liniile din spațiu se intersectează (fig. 2.26, b).


Pentru a determina dacă este sau nu se intersectează în mod direct, este suficient pentru a satisface această condiție pentru două proeminențe. O excepție este cazul în care una dintre liniile care se intersectează este un nivel de profil. În acest caz, pentru a verifica intersecția liniilor necesare pentru a construi un profil de proiecție.
Să prin punctul A este necesar să se efectueze pe orizontală b. care intersectează linia a (fig. 2.27, a). Pentru a face acest lucru, țineți punctul A2 prin b2 # 9553; x12 (etapa 1), la intersecția cu punctul a2 K2 (ris.2.27 b). În continuare, folosind link-ul de proiecție a1 pentru a găsi K1 punctul (etapa 2) și conectarea punctelor A1 și K1 (etapa 3), obținem b1.

Fiecare punct de intersecție este proiecția a două puncte care fac parte din dreapta; Aceste două puncte sunt proiectate pe o grindă și numită afirmație.


Punctele K și L (fig. 2.28, a) se află pe aceeași grindă orizontală este proiectată. Proiecția orizontală a punctelor sunt aceleași și la intersecția proeminențelor a1 orizontale și liniile b1. Punctul Ka. litera L b. Se poate observa că punctul K deasupra punctului L. Se crede că, atunci când este proiectat pe punctul P1 K este vizibil, iar punctul L - invizibil (ascuns dintr-un punct de observator K).
Punctele M și N minciună pe aceeași grindă frontală proiectată (fig. 2.28, b). Puncte de proiecție frontale coincid și se află la intersecția proiecțiilor față a2 directă și b2. Punctul M o. litera N b. N punct suplimentar de la P2. .. punctul M. decât adică, mai aproape de ochii observatorului și, prin urmare, atunci când se proiectează P2 punct de pe N vizibil, în timp ce punctul M - nu sunt vizibile. Desemnări puncte invizibile ale previziunilor din paranteze.