Unghiul solid - a spațiului, care este unirea tuturor căilor. provenind de la un punct dat (unghiul la vârf) și se intersectează o suprafață (care se numește o suprafață subîntinzând un unghi solid dat). Cazuri particulare ale unghiului solid este unghiurile triquetrous și poliedrice. Granița unghiului solid este o anumită suprafață conică.
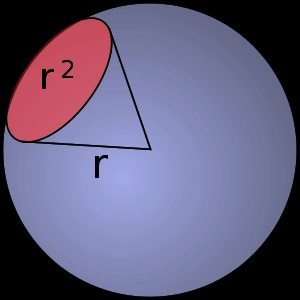
Unghiul solid măsurat prin raportul dintre aria unei sfere cu centrul de la vârful unghiului, care este străbătută de acest unghi solid la o rază pătrată a sferei :. $$ \ Omega \, = \, $$
Evident, unghiurile solide sunt măsurate cu numere abstracte () fără unități. Unitatea unghi solid în SI (unități de sistem) este steradian. egal cu unghiul solid al suprafeței tăiate a unei unități de sferă cu o suprafață de 1 unitate pătrat. sferă completă formează un unghi solid de steradian 4π (unghi solid total) pentru nodurile situate în interiorul sferei, în special, pentru centrul sferei; astfel încât este unghiul solid subîntins de orice punct al suprafeței închise, această suprafață este complet acoperită, dar nu îi aparține. Mai mult decât atât unghiul solid steradian poate fi măsurat în grade, pătrat, pătrat și secunde pătrat minut, și, de asemenea, în fracțiuni de unghi solid plin.
Un unghi dublu solid într-un unghi solid dat definit ca unghiul Ω, constând din grinzi ce formează grinda cu orice unghi Ω unghi ușor.
Unitate Coeficienți de conversie unghi solid.
Calcularea unghiurilor solide [modifică]
Pentru o subîntind suprafață arbitrară \ (S \) unghi solid \ (\ Omega \), sub care este vizibil de origine, este egală cu
unde \ (r, \ vartheta, \ varphi \) - coordonatele sferice ale suprafeței elementului \ (dS, \) \ (\ mathbf \) - raza vectorului, \ (\ mathbf \) - un vector unitate normală la \ (dS . \)
Proprietățile unghiurilor solide [modifică]
- Unghiul solid complet (sferă completă) este egal cu \ (4 \ pi \) steradian.
- Suma tuturor unghiurilor solide, unghiuri solide interioare duble ale unui poliedru convex. Acesta este egal cu unghiul totală.
Valorile anumite unghiuri solide [modifică]
- Triangle cu vertex coordonatele \ (\ mathbf_1 \) \ (\ mathbf_2 \) \ (\ mathbf_3 \) este vizibil din originea într-un unghi solid
\ (\ Omega = 2 \, \ mathrm \, \ frac_1 \ mathbf_2 \ mathbf_3)> _ 1 \ cdot \ mathbf_2) r_3 + (\ mathbf_2 \ cdot \ mathbf_3) r_1 + (\ mathbf_3 \ cdot \ mathbf_1) r_2> \ )
unde \ ((\ mathbf_1 \ mathbf_2 \ mathbf_3) \) - mixte vectori de date de produs, \ ((\ mathbf_i \ cdot \ mathbf_j) \) - produsul scalar al vectorilor corespunzători sunt indicate în vectori aldine font normală - lungimea lor. Folosind această formulă se poate calcula unghiurile solide subîntins poligoane arbitrare ale nodurilor cu coordonate cunoscute (este suficient pentru a împărți poligon în triunghiuri care nu se suprapun).
- Unghiul solid la vârful unui con circular drept cu un unghi α soluție \ egal (\ Omega = 2 \ pi (1 -<\href<\texttip <\cos><Косинус>>> \ frac) \). Dacă cunoscută raza de bază \ (R \) și înălțimea \ (H \) al conului, de \ (\ Omega = 2 \ pi (1 - \ frac>) \). Atunci când unghiul conului este mic, \ (\ Omega \ approx \ frac \) (\ (\ alpha \), exprimată în radiani) sau \ (\ Omega \ circa 0,000239 \ alpha ^ 2 \) (\ (\ alpha \ ) exprimat în grade). Astfel, unghiul solid care poate fi văzută din (diametrul lor unghiular aproximativ egal cu 0,5 °) Pământ Luna si Soare, este de aproximativ 6 × 10 -5 steradian sau zona ≈0,0005% din sferei cerești (adică unghiul solid total) .
- Unghiul solid la vârful cubului (sau orice alt paralelipiped dreptunghiular) este egal cu \ (\ frac \) al unghiului solid total sau \ (\ frac \) steradian.