1. Integrare directă
Prin integrarea directă realiza o astfel de metodă de integrare, în care transformarea integrală prin integrantul și utilizarea proprietăților integrale nedefinite identică este una sau mai multe integralele tabelare.
Exemplul 1. Găsirea
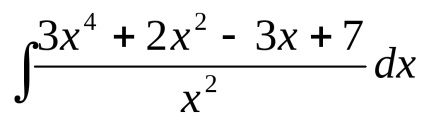
Împărțind numărătorul de numitor, obținem:
=
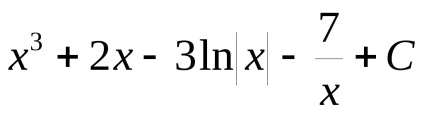
Rețineți că nu este necesar, după fiecare termen pentru a stabili o constantă arbitrară, astfel încât suma lor este, de asemenea, o constantă arbitrară pe care le scrie la sfârșitul anului.
Exemplul 2. Găsirea
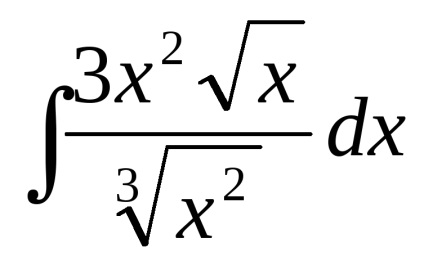
transforma integrantul după cum urmează:
.
Aplicarea integrală intabulat 1, obținem:
.
.
.
=
=.
În unele cazuri, găsirea integrala simplifică utilizarea unor metode artificiale.
Exemplul 6. Căutare
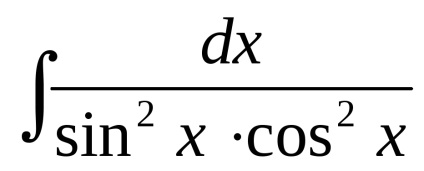
înmulțirea integrandul pentru a găsi
= .
.
.
2. Integrarea prin înlocuirea variabilei
Se calculează având în vedere integrarea integrală directă nu este întotdeauna posibil și, uneori, acest lucru implică mari dificultăți. În aceste cazuri, utilizați alte tehnici. Una dintre cele mai eficiente este metoda de schimbare a variabilei. Esența ei constă în faptul că, prin introducerea unei noi variabile de integrare poate fi redusă dat integrantă noului, care este relativ ușor de luat în mod direct. Există două versiuni ale acestei metode.
a) Metoda sumãrii funcționează sub semnul diferenței
Prin definirea diferențial.
Mutarea în această ecuație de la stânga la dreapta sunt numite „factor de însumarea
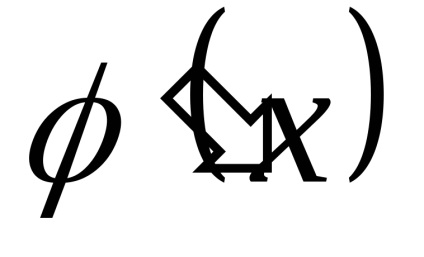
Teorema pe invarianța formulelor integrale
Orice formulă de integrare își păstrează forma atunci când înlocuiește variabila independentă a oricărei funcții diferențiabile a acesteia, și anume, dacă
unde
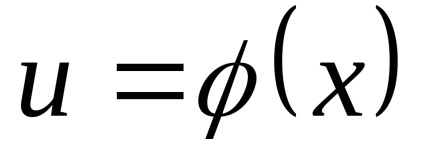
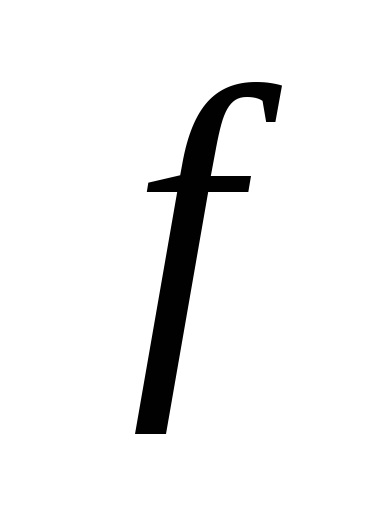
Din ceea ce ar trebui
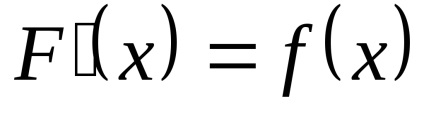
.
Să presupunem că doriți să calculeze integrala
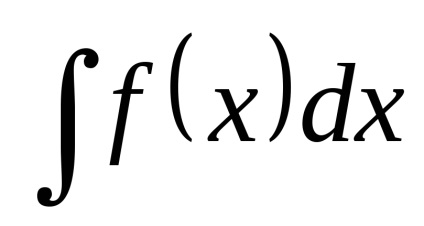
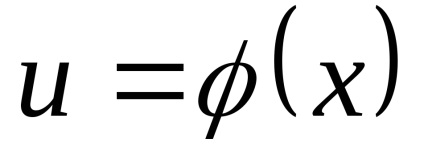
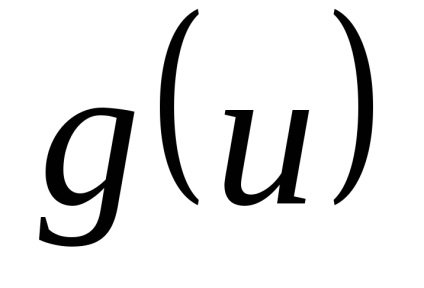
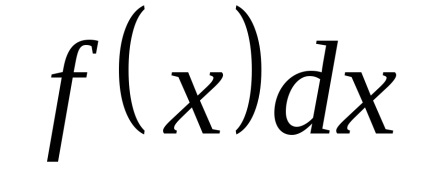
.