Figura deplasare formată prin rotirea în jurul trapezului curbate axa Ox delimitate de o continuă curba y = f (x) (a ≤ x ≤ b), liniile axei Ox și x = a și x = b, este dată de:
La fel, volumul figurii format prin rotirea în jurul axei trapezului curbat Oy delimitată de o curbă y continuu = # 966; (x) (c ≤ x ≤ d), liniile Axei Ox și y = c și y = d, este dată de:
Exemplul №1. Se calculează volumele figurilor formate de spațiul de rotație delimitată de liniile menționate anterior.
y 2 = 4x; y = 0; x = 4.
integrare limite a = 0, b = 4.
Exemplul №2. y 2 = 4x; y = x
Construiește cifra. Rezolva sistem:
y 2 = 4x
y = x
găsi punctul de intersecție al parabolei și o linie dreaptă: O (0, 0), A (4, 4).
În consecință, limitează integrarea a = 0; b = 4. Suma cautata reprezintă diferența dintre V1 volumul paraboloidului format prin rotirea curbei y 2 = 4x. și V2 volumul conului format prin rotirea unei linii drepte y = x:
Exemplul №3. Se calculează volumul solidului obținut prin rotirea în jurul figurii axei Ox delimitate de o linie dreaptă y = x și parabolei.
Vom găsi intersecția liniilor. Pentru a face acest lucru, vom rezolva ecuația. Obținem x1 = 0, x2 = 1.
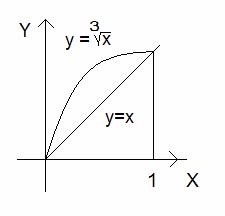
Fig. 2. Valoarea de rotație a corpului.
Volumul corpului poate fi calculată în conformitate cu formula unde
, f2 (x) = x.
.
Raspuns :.