Viteza unghiulară și accelerația unghiulară a corpului sub formă de cantități vectoriale
Dovada unor teoreme ale cinematicii și dinamicii, dacă luăm în considerare viteza unghiulară și accelerația unghiulară ca mărime vectorială poate fi simplificată. Vector (fig. 49), care arată viteza unghiulară, este construit pe axa de rotație, el de ghidare de-a lungul axei de cealaltă parte, să caute la capătul său, pentru a vedea ce se întâmplă invers acelor de ceasornic roti. Începe poate fi plasat în orice punct al axei, - un vector de alunecare. modul | | = | Dφ / dt | = | | Aceasta este egală cu valoarea absolută a vitezei unghiulare.
E
Dacă să preia unitatea de axa vectorul z -












Vectorul poate coincide cu direcția, poate fi diferit. Dacă accelerația de rotație, ambii vectori au aceeași direcție (figura 50.), În cazul în care lent - în diferite (Figura 51.).
Folosind conceptele vitezei unghiulare vectorului și accelerația unghiulară, vom exprima viteza liniară și accelerația liniară în formă de produse vectoriale.
Viteza liniară de expresie și accelerația ca vector
Să presupunem că avem un corp de rotație în jurul unei axe fixe. Zugrăvi viteza sa unghiulară și accelerația unghiulară ca vectori. Începutul moșiile lor, până la punctul în jurul axei de rotație. Ia orice punct din corpul lui M. Din punct de pe vectorul raza punctului M. Unghiul dintre axa z și este notat cu α. Arătăm că punctul M vectorului de viteză liniară.
Acest lucru poate fi ușor de verificat amintind definiția produsului transversală a doi vectori. Produsul transversală a doi vectori este un nou vector perpendicular pe planul în care se află vectorul două date, și este egal cu modulii modulo produs prin sinusul unghiului între acestea. Vectorul (fig. 52), perpendicular pe planul și este ΔOMO1 ωr păcat α = ωR (R = r păcat α din ΔOMO1).
liniar vector viteza v = ω R. R. și direcționată perpendicular adică ΔOMO1 plan în direcția de rotire, și este invers acelor de ceasornic. Prin urmare, vectorii și sunt egale, după cum este necesar.
- formula de bază de cinematică sau formula lui Euler.
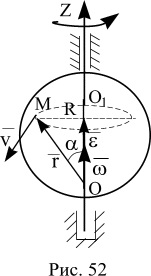
Un vector este suma celor doi vectori. Arătăm că - acolo āτ. - aN - vectori ai tangenta și accelerația normală. Vector modulo egal păcat εr α = εR și direcționată perpendicular pe planul în care se află ambele, adică ΔOMO1 avionul. De aceea, este un vector perpendicular pe raza de rotație și o accelerație unghiulară egală cu produsul cu raza de rotație, adică, Acest vector este āτ.
vector modulo egal β ωv sin β = 90 Nr și ωv păcat β = ωv = ω 2 R. deoarece v = ω R.
El a direcționat perpendicular pe planul în care se află, și că este radial spre centru (fig. 53).
Exemplu. Pe scripete rază R = 0,5 m Screw tors, capătul liber al cărui sarcină suspendată A (fig. 54). Sarcina este coborâtă uniform accelerat din repaus cu accelerație aA = 2 m / s 2 și rotește roata de transmisie. Găsiți legea mișcării de rotație a roții de curea, viteza unghiulară, accelerația unghiulară în orice moment t. precum și viteza și accelerația punctului M aM situată pe marginea fuliei. Georgia se deplasează cu o accelerație uniformă, astfel încât să puteți găsi viteza vA = AAT = 2t m / s. Viteza de încărcare egală cu viteza punctelor jantei, adică Vm = vA = 2t. atunci ω = Vm / R = 4t c -1. unghiulară accelerație ε = dω / dt = 4 c -1. și anume ε = const și rotirea fuliei uniform accelerată. ω0 = 0, și, prin urmare, rotația legii:
unelte ordinară
Mișcarea de rotație este larg răspândită într-o varietate de mașini și mecanisme. Rotația poate fi transmisă pe o distanță prin intermediul conexiunilor flexibile (centuri de transfer), sau prin contact direct (sau unelte fricțional). Centura si frictiune folosit forța de frecare, și o roată dințată - angrenare mecanică. În fiecare dintre aceste tipuri de programe are un element de conducere care informează mișcarea, iar elementul de antrenare, care se obține din mișcarea elementului de conducere. Luați în considerare un tren de roți dințate serie sau o serie de compuși unelte.
Compuse angrenaje ale căror arbori rotesc în lagăre fixe numite compus obișnuit sau un angrenaj obișnuit (fig. 55).
Distanța dintre doi dinți adiacente se numește treaptă de viteze h.
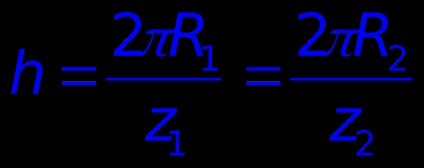
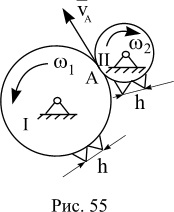
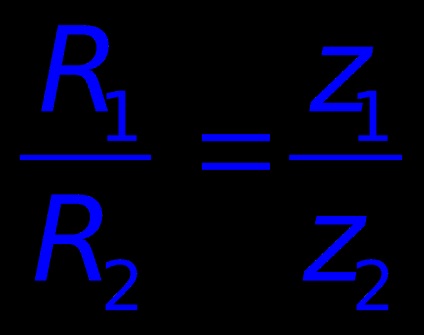
în care R1. z1 - rază și numărul de dinți de roată I; R2. z2 - rază și numărul de dinți de roată II.
transmisie obișnuită se caracterizează prin raportul de transmisie. raportul de transmisie al I1,2 raportul de transmisie este egală cu viteza unghiulară a co 1 roții motoare la w2 viteza unghiulară determinată. i1,2 = ω1 / ω2.
Dacă n este roțile, multinodală raportul de transmisie al unui raporturi de transmisie egală cu produsul de perechi legate:
în cazul în care m - numărul de link-uri externe.
Atunci când o angrenare interioară (. Figura 56), raportul de transmisie este pozitiv, în timp ce exterior - negativ.
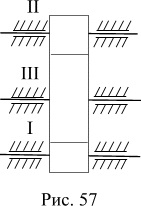
roți dințate este format din trei roți dințate (Fig. 57). Prima roată are un diametru de 0,2 m și face 7200 rot / min. A doua roată - 4000 rot / min, iar al treilea - 600 rot / min. Definirea diametrele doua și a treia roți.
Nu există nici un răspuns corect.
Raza de 0,8 m pe pneuri, care se rotește cu accelerație constantă în timpul accelerării dintr-un impas, în timp ce angajat 750 revoluții. Se determină timpul de rampă, în cazul în care viteza de puncte pe janta atins cu 200 m / s.
Raza Roata 0,5m, în timp ce rotirea accelerat în mod uniform, 10 are o viteză unghiulară n = 120 rot / min (n0 = 0). Se determină accelerarea punctului A a jantei la momentul t = 1 min.
Mâner OA (fig. 58) este rotită cu legea φ = 5t. Pentru a determina cât de mult de încărcare se ridică la o înălțime de 5 m, în cazul în care r1 = 0,2 m; r2 = 0,3 m; r3 = 0,15 m.
Rotirea corpului în jurul unei axe fixe definită de ecuația φ = 1,5t 2 - 4T. Se determină viteza și accelerația corpului un punct distanțat față de axa de rotație de 0,2 m, la momentul t1 = 2.
elev forme neseparat de învățământ este format din următoarele etape majore: fizica samostoyatelnoeizuchenie de uchebnymposobiyam. tverdogotela mișcare în raport cu o axă fixă. Dacă I = const, atunci M = I, în care - accelerația unghiulară a corpului. 26.
elev forme neseparat de învățământ este format din următoarele etape majore: fizica samostoyatelnoeizuchenie de uchebnymposobiyam. tverdogotela mișcare în raport cu o axă fixă. Dacă I = const, atunci M = I, în care - accelerația unghiulară a corpului. 26.
manualele
- uchebnoeposobie. cu aparate didactice speciale, contribuind la locul de muncă individuale ale studenților cu privire la dezvoltarea subiectului; Tutorial - uchebnoeposobiedlyasamostoyatelnogoizucheniya.
Stat Standard Educațional
studiu. tverdogotela 1.2 Tema 2: Dinamica Dinamica punctelor materiale ale unui punct și de translație de mișcare tverdogotela materialului. TVERDOGOTELAKinematika. Shahin EL Fizica: munca Uchebnoeposobiedlyasamostoyatelnoy de elevi / 3rd ed.
studiu. tverdogotela 1.2 Tema 2: Dinamica Dinamica punctelor materiale ale unui punct și de translație de mișcare tverdogotela materialului. TVERDOGOTELAKinematika. Shahin EL Fizica: munca Uchebnoeposobiedlyasamostoyatelnoy de elevi / 3rd ed.