Funcția densitate de probabilitate teoretică 1. Definiție. Reprezentarea grafică a distribuțiilor empirice și teoretice
distribuția densității a încrederii speranța matematică
La construirea histograme și poligoane pe axa absciselor reprezintă valori ale rezultatelor măsurătorilor (intervale mid xi), axa verticală - apariția unor anumite date măsurate în fiecare interval i-lea.
Din cauza numărului limitat de rezultate de măsurare în timpul procesării în loc de așteptarea și variația medie obținută lor empirică aproximativă, respectiv otsenki-
și varianța empirică S 2. caracterizează media rezultatelor măsurării și a gradului de variațiile măsurătorilor.
și S 2 sunt determinate din expresiile:
Valorile probabilității ca rezultatul unei măsurători la un anumit interval poate fi determinat prin utilizarea valorii funcției:
,
.
Apoi, probabilitatea de a obține rezultatul în intervalul i din valoarea lui h
.
Vom face toate calculele din tabel și pe baza acestor rezultate vom construi o curbă de distribuție teoretică, precum și histograma și poligon de distribuție empirică:
Interval xi Mid
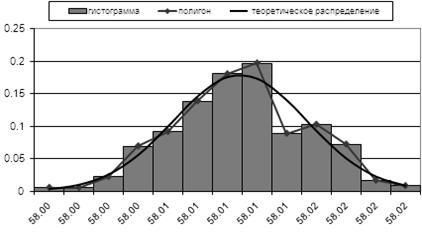
consimțământul 2.Kritery distribuțiilor empirice și teoretice
Se crede că distribuția empirică este de acord cu bine teoretic, dacă (1 - g) este mai mare de 0,1. Potrivit criteriului Kolmogorov, comparând valorile empirice și teoretice, dar nu și distribuția densității, și funcțiile integrate. Maxim (valoare absolută) a diferenței între acestea DN substituite în expresia:
,
unde N - mărimea eșantionului.
Calculul F'i valori empirice și teoretice ale integralei fabricarea funcției Fi prin însumarea valorilor secvențial respectiv P'i și Pi. Rezultatele de calcul sunt prezentate pe scurt în tabelul de mai jos:
Pentru lN = 0,52 g »0,05 Þ (1 - 0,05) = 0,95> 0,1.
De aici putem trage concluzia că acordul de distribuție empirică cu teoretice normale poate fi considerată bună.
intervale de încredere 3.Opredelenie
În unele probleme, mai ales atunci când un număr mic de măsurători, este necesară nu numai pentru a găsi o evaluare empirică pentru un parametru, dar, de asemenea, pentru a determina intervalul de încredere în care un nivel de încredere va fi valoarea teoretică.
Intervalul de încredere pentru așteptarea determinat de expresia:
interval de încredere Integral
Valorile t # 947; tabelate și este egală cu t # 947; = 2,18 pentru N = 13 și # 947; = 0,95.
Intervalul de încredere pentru deviația standard se determină din expresia:
sens # 967, 1 februarie. # 967, 2 februarie tabelate și se determină în funcție de numărul de măsurători N și probabilități unilaterale # 947; 1. # 947; 2:
valoare # 967, 1 2 calculează la probabilitate (1- # 947; 1) # 967; 2 2 - când # 947; 2.