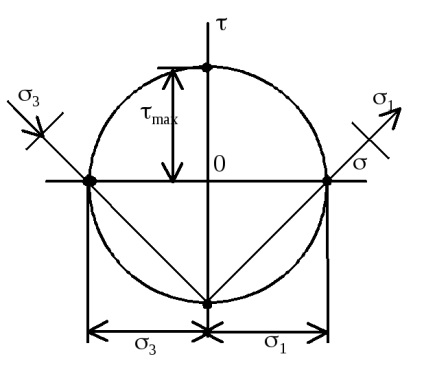
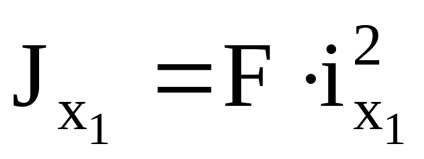B
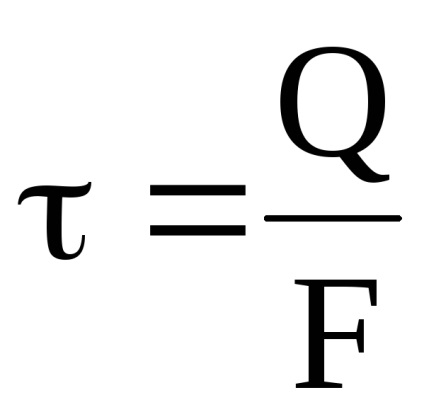
P
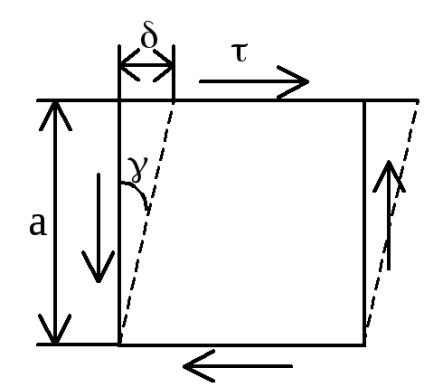

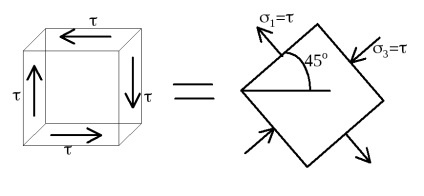
legea lui Hooke la forfecare. = / G sau = G.
G - modul de forfecare sau modul de forfecare [MPa] - constanta materialului ce caracterizează capacitatea de a rezista la deformare la forfecare.
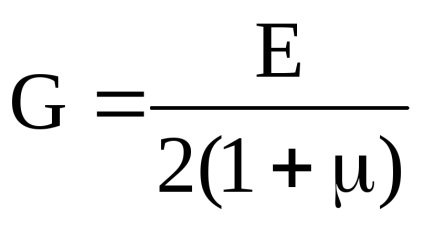
Energia potențială de forfecare:
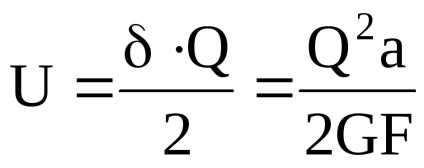
Energia specifică tulpinii la forfecare:
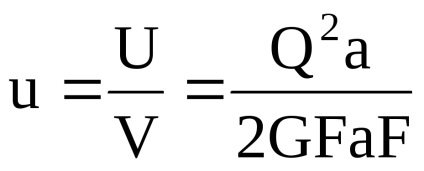
unde V = aF - elementul de volum. Având în vedere legea lui Hooke,
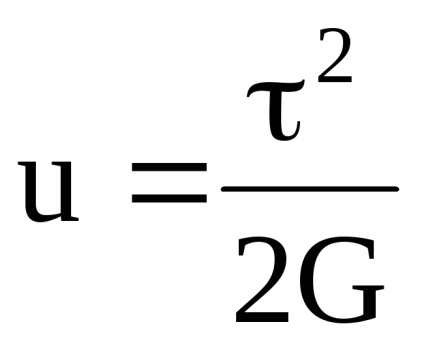
Toate energia potențială este consumată în forfecare pură doar la modificarea formei, volumului schimbare sub deformarea de forfecare este zero.
K
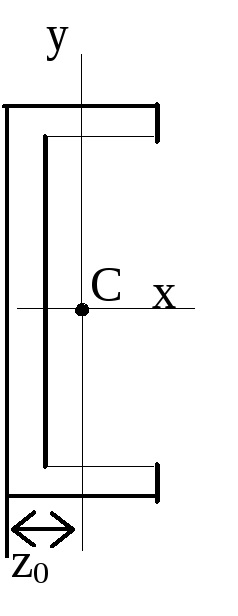
Caracteristicile geometrice ale secțiunilor plane
Zona.
C
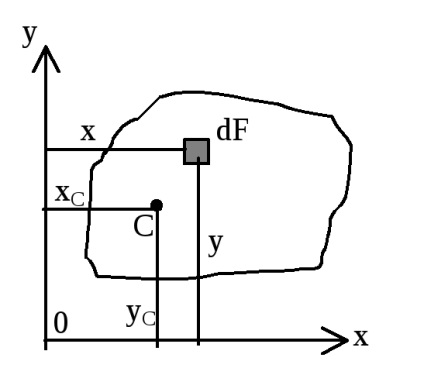
Rezumând (integrarea) astfel de lucrări pe parcursul figurilor obține pătrat momente statice în jurul axelor y și x:

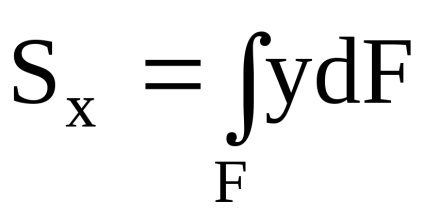
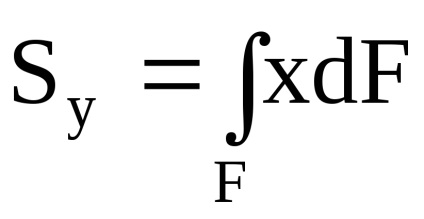
centrul de greutate coordonate:
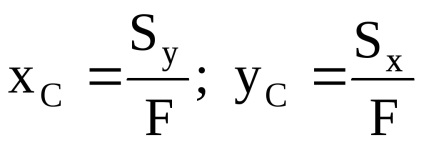
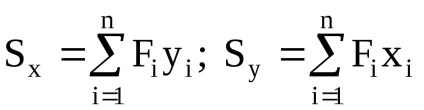
Coordonatele centrului de greutate al unui complex figura:
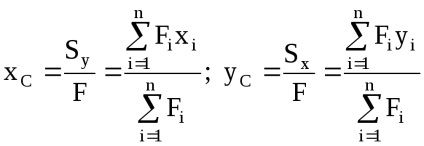
M
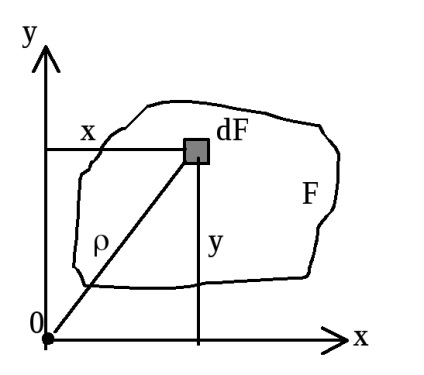
Axial (ecuatorial) moment de inerție - suma produselor zonelor elementare df în pătrate de distanțele lor față de axa.
Polar momentul de inerție în raport cu un punct (pol) - suma produselor din zonele elementare pe pătratele distanțelor de la acest punct.
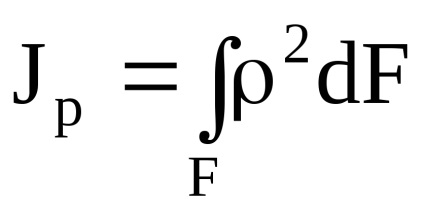
Un moment de inerție centrifugal - suma produselor din zonele elementare de pe distanțele lor de la două axe perpendiculare între ele.
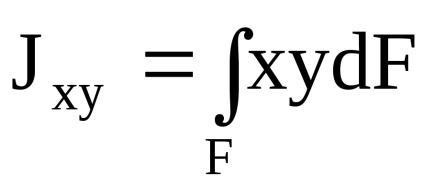
Un moment de inerție centrifugal în jurul axelor, dintre care una sau ambele coincid cu axele de simetrie, este zero.
Axială și momentele polare de inerție sunt întotdeauna pozitive, momentele de inerție centrifugale poate fi pozitiv, negativ sau zero.
Momentul de inerție a unei figuri complexe este suma momentelor de inerție ale pieselor compozite.
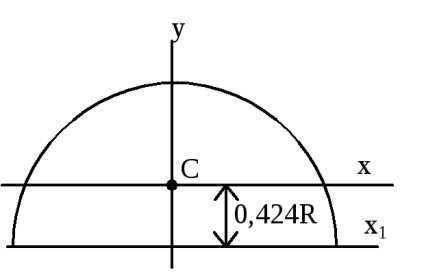
Momentul de inerție al formei sale simple
P
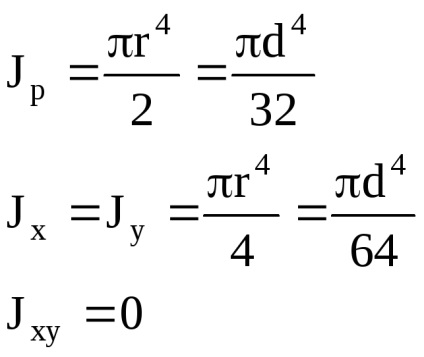
M
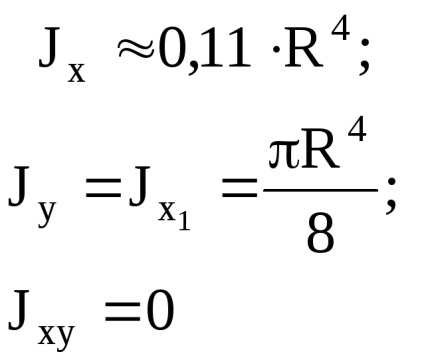
D
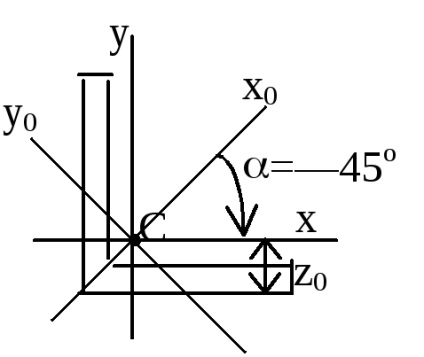
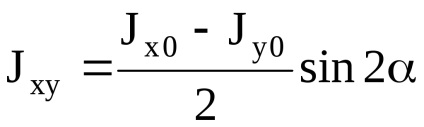
inerție omenty în jurul axelor paralele:
moment de inerție în jurul oricărei axe egală cu momentul de inerție în jurul unei axe centrale paralelă cu aceasta, plus produsul dintre piesele pătrate pe distanța pătratică între axe. Jy1x1 = Jyx + Abf; ( „A“ și „b“ sunt substituite în formula dată semnul lor).
Relația dintre momentele de inerție la rotirea axe:
J
Jx1y1 =
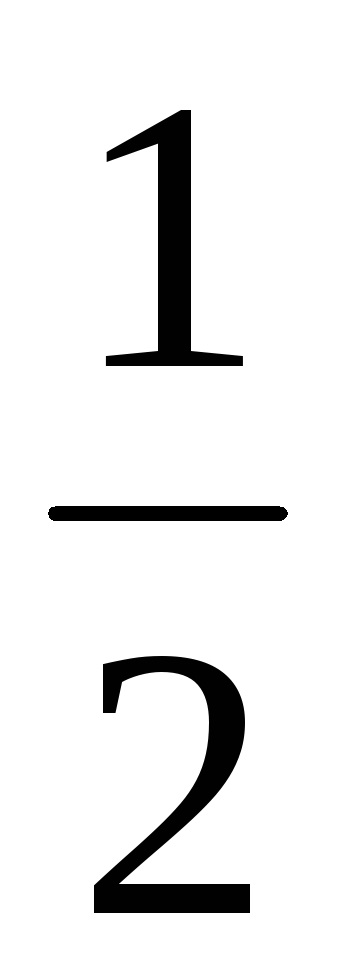
Unghiul > 0, în cazul trecerii de la vechiul la noul sistem de coordonate are loc împotriva chas.str. Jy1 + Jx1 = Jy + Jx
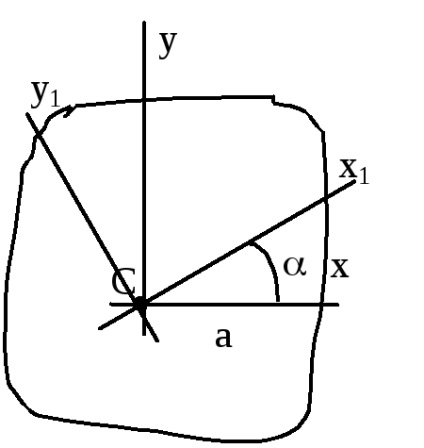
Extreme (minime și maxime), valori ale momentelor de inerție sunt numite momentele principale de inerție. Axele despre care momentele de inerție axial au valori extreme, numite axele principale de inerție. Axa principală de inerție reciproc perpendiculare. momente centrifugale de inerție axelor principale = 0, adică, axe principale de inerție - axa în jurul căreia momentul de inerție centrifugal = 0. Dacă una sau ambele axe coincide cu axa de simetrie coincid, ele sunt cele principale. Unghiul care definește poziția axei principale:
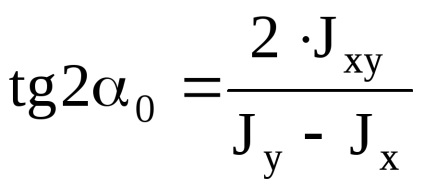
Jmax + Jmin = Jx + Jy. Un moment centrifugal de inerție față de axele centrale principale de inerție este egal cu 0. Dacă sunt cunoscute momentele principale de inerție, trecerea la formula rotit axe:
cos Jx1 = Jmax 2 + Jmin păcatul 2 ; cos Jy1 = Jmax 2 + Jmin păcatul 2 ; Jx1y1 =
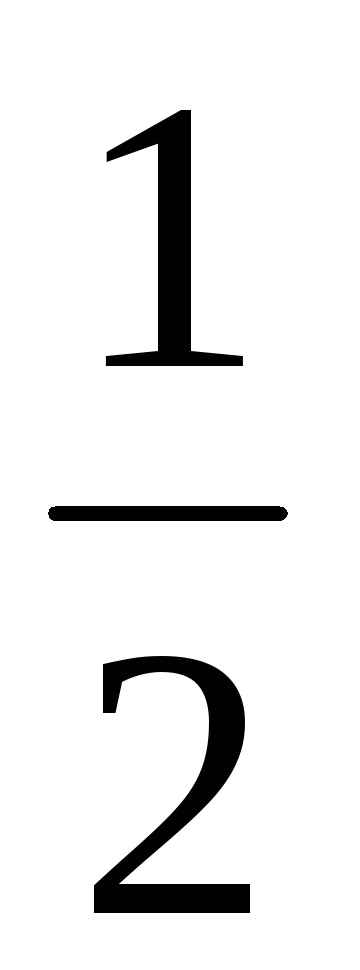
Scopul final al calculării caracteristicilor geometrice ale secțiunii este de a defini principalele momente centrale de inerție și poziția principalelor axe centrale de inerție. P
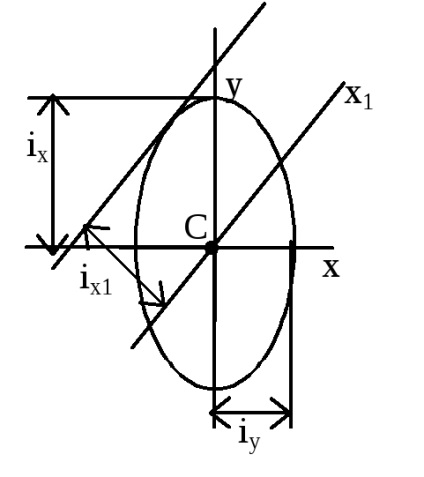
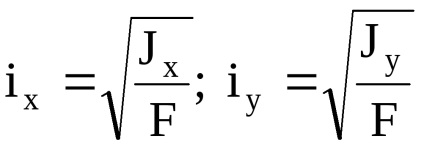
Dacă JX și JY momentele principale de inerție, IX și iy - razele principale de girație. Elipsă, construit pe razele principale de inerție a ambelor semi-axe se numește elipsa de inerție. Folosind elipsa de inerție poate fi găsită raza grafic ix1 de inerție pentru orice axă x1. În acest scop, este necesar să se elaboreze o tangentă la elipsă paralelă cu axa x1. și se măsoară distanța de la această axă la tangenta. Cunoscând raza de girație, puteți găsi un moment de inerție în raport cu axa X1.