Subiect: „forțe interne în secțiunile transversale ale barei“
1. Suporturile și reacțiile de suport și definirea acestora
2. Forța transversală și momentul de încovoiere
3.Vzaimosvyaz între momentul încovoietor, forța de forfecare și de sarcină distribuită de intensitate
Reacțiile 1.Opory și de sprijin și definirea acestora
La calcularea elementelor de construcții găsite în principal se confruntă cu flexiune. Tijele de rulare numite grinzi predominant flexiune. Pentru a fasciculului ar putea fi încărcat și transmite-l la baza, acesta trebuie să fie conectat cu el poartă obligațiuni. În practică, utilizează mai multe tipuri de link-uri de referință, sau cum se spune, mai multe tipuri de suporturi.
Există trei tipuri principale de sprijin:
a) balamale mobile suport:
b) în comun fixe de sprijin:
c) de ancorare.
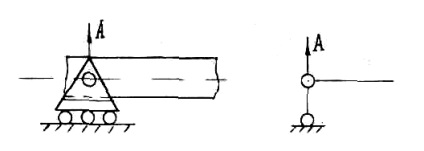
Fig. 1 prezintă un suport pivotabil-mobil, un astfel de sprijin permite fasciculului să se rotească liber și deplasa în direcția orizontală. Prin urmare, reacția în suportul va fi una forță verticală. Simbolul un suport arată în partea dreaptă.
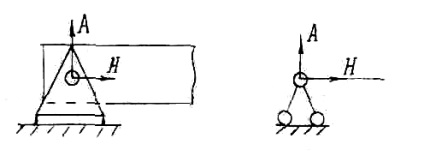
Fig. 2 prezintă rulment fix-balama. Acest suport permite fasciculului să se rotească liber, dar nu se poate mișca. Prin urmare, pot exista două reacții - forțele verticale și orizontale. Ele pot fi pliate în sus și de a lua o forță rezultatiruyuschuyu, dar este necesar să se cunoască unghiul de rostral va fi trimis. Mai convenabil de a utiliza componentele verticale și orizontale ale reacției.
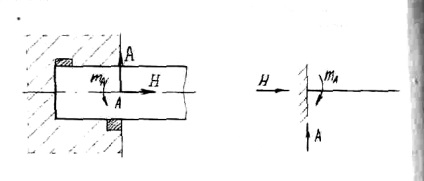
Fig. 3 prezintă punctul de ancorare. Ea nu permite nici un fascicul rotit sau mutat. Prin urmare, pot exista trei reacții de sprijin: În prezent, forțele verticale și orizontale. În cazul în care fasciculul nu are un efect asupra final, această parte a numit-o consolă.
Definiți suporturi pentru reacția fasciculului (vezi. Fig. 4).
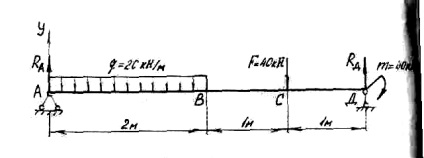
Suportul și reacția orizontală este zero deoarece q sarcină distribuită și forța F concentrată au direcție verticală. reacții de sprijin
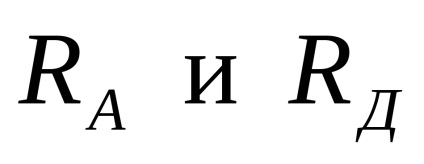
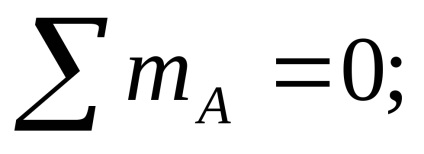
unde
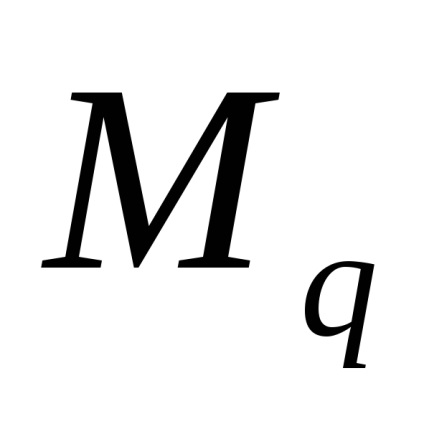
Produsul q de distanța la care se aplică, starea de echilibru a sistemului este egală cu forța concentrată aplicată în mijlocul segmentului. Prin urmare, timpul
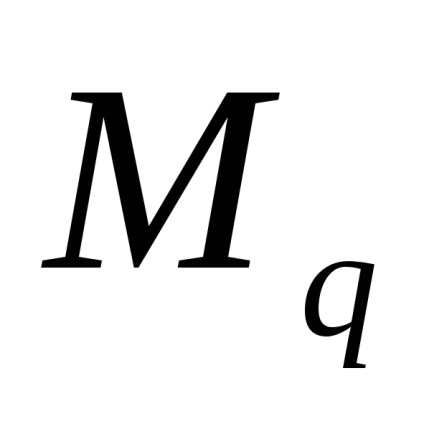
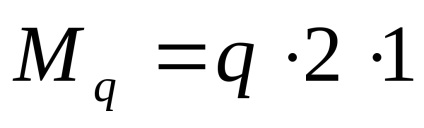
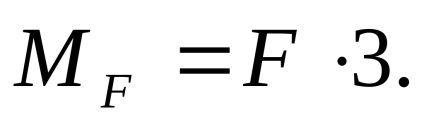
momentul extern m la umăr nu este multiplicat, ca o pereche de forțe, și anume, două egale în mărime, forțele direcționate opus, care au un umăr uniform.
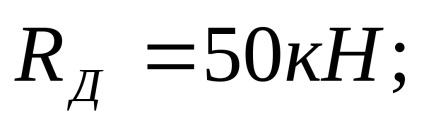
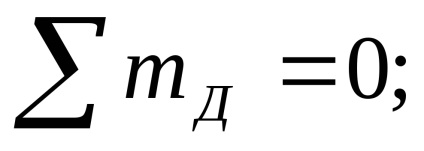
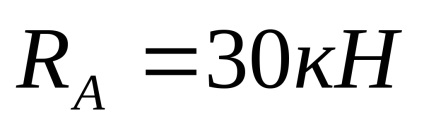
Testarea: Suma tuturor forțelor de pe axa Y verticală trebuie să fie egală cu zero:
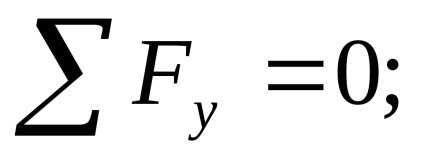
.
Moment m în starea de echilibru static
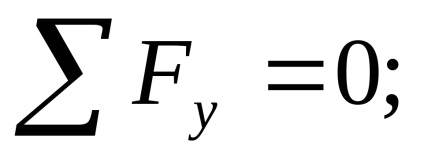
Reacțiile sunt definite corect.
2. Forța transversală și momentul de încovoiere
Lăsați actul de forțe fascicul
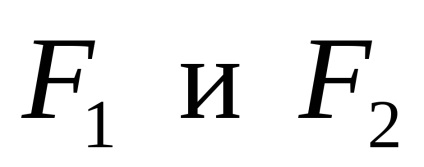
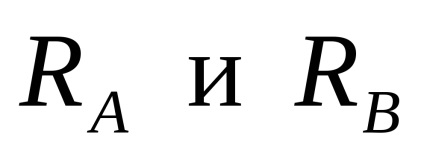
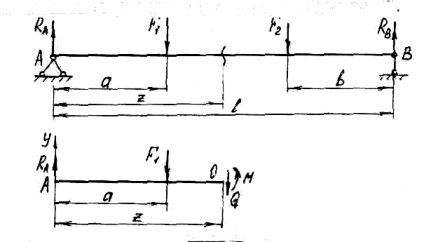
Din moment ce toate forțele externe, care acționează pe verticală, componenta orizontală a reacției podelei la A nu va. Fasciculul nu se va micșora sau întinde, și anume forța longitudinală în secțiunile transversale este zero. Ai putea lua un exemplu, atunci când forțele
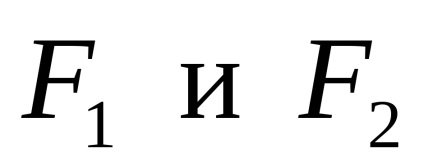
Deoarece forțele externe
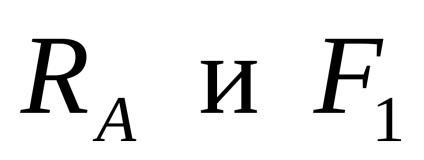
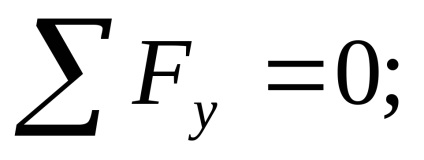

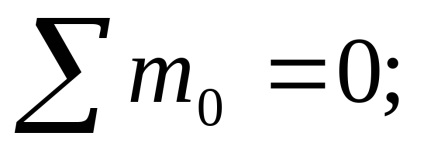
.
Concluzie: Forța de forfecare la secțiunea numerică suma ravnaalgebraicheskoy a tuturor forțelor externe și a momentelor de încovoiere momentsumme toate calculate cu referire la iprilozhennyh secțională considerată parte a fasciculului.
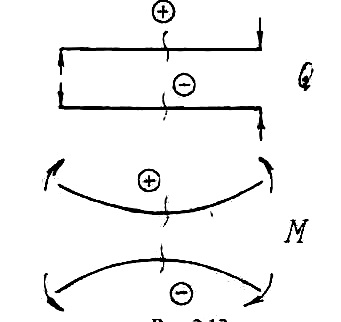
Pentru forțe transversale și momente de încovoiere face reguli obligatorii de semne (vezi. Fig. 6).
În cazul în care forța este încercarea de a transforma partea considerată a fasciculului în sensul acelor de ceasornic, atunci este o forță laterală pozitivă, și, dimpotrivă, în cazul în care acționează în sens antiorar forța laterală este negativă. Fig. 5 puterea
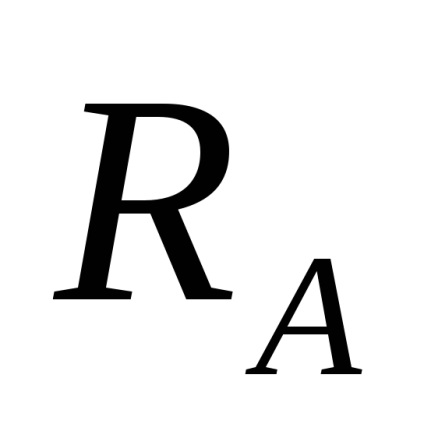

Dacă forța externă sau fascicul de cuplu exterior este îndoit în jos convexitate, moment pozitiv apariția îndoire, și invers, o convexitate negativă în sus .
3. Relația dintre incovoietoare,
forță transversală și de sarcină distribuită de intensitate
Lăsați o grindă în consolă (vezi. Fig. 7) operează sarcină distribuită care variază de-a lungul lungimii grinzii. La o distanța z de la capătul din stânga al preluării dz segmentul infinitezimal.
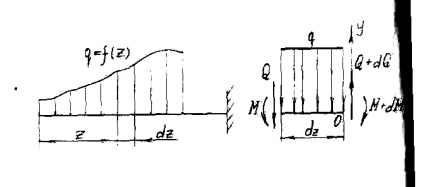
Apoi, distribuția sarcinii pe ea poate fi considerată ca fiind constantă. Pe partea stângă a segmentului în cauză sunt forțe interne Q și M pe dreapta având în vedere incrementul forțelor Q interne + dQ și M + dM.
Ecuația de echilibru static pentru a forma lungimea fasciculului:
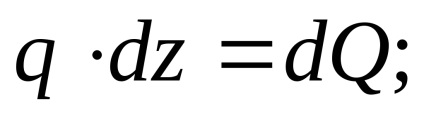
Un al treilea termen poate fi neglijată ca o infima de ordin superior, adică.:
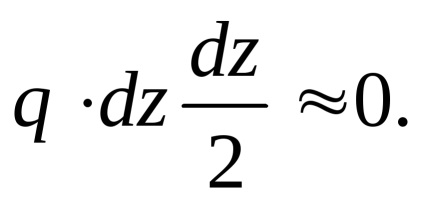
După transformări obținem:
și anume prima derivată a momentului de încovoiere pe abscisă (lungimea grinzii) este forța de forfecare.
Dacă în formula (1), pentru a înlocui valoarea Q din formula (2), obținem:
și anume derivata a doua a momentului de încovoiere este distribuită intensitate de încărcare.