Elemente de teoria erorilor
Numărul exact și aproximativă
Precizia de obicei, nu există îndoieli, atunci când este vorba de valori număr întreg de date (2 creion 100 de copaci). Cu toate acestea, în majoritatea cazurilor în care valoarea exactă a numărului nu poate fi specificat (de exemplu, linia de subiect al măsurării, eliminarea rezultatelor de instrument, etc), avem de-a face cu datele aproximative.
Valoarea aproximativă este un număr diferă puțin de valoarea exactă și îl înlocuiește în calcule. Gradul de valorile aproximative ale diferențelor față de valoarea exactă se caracterizează printr-o eroare.
Există următoarele surse majore de eroare:
1. Erori de formulare a problemei. apărute ca urmare a unei descriere aproximativă a fenomenelor reale în termeni de matematică.
2. Erori ale metodei. asociată cu dificultatea sau incapacitatea de a rezolva problema și înlocuirea acesteia cu o structură similară, astfel încât a fost posibil să se aplice un bine-cunoscut și accesibile soluții de metodă și de a obține rezultate în apropierea țintei.
3. Eroare fatală. asociate cu valori aproximative ale datelor de intrare și rezultă din calculele de mai sus numerele aproximative.
4. eroare de rotunjire. Valorile asociate cu rotunjirii datelor de intrare, rezultatele intermediare și finale, obținute prin utilizarea mijloacelor de calcul.
Eroare absolută și relativă
Contabilizarea erorilor este un aspect important al aplicării metodelor numerice, deoarece eroarea rezultatului final al soluției întreaga problemă este un produs al interacțiunii tuturor tipurilor de erori. Prin urmare, unul dintre principalele obiective ale teoriei erorilor este precizia de estimare a rezultatului bazat pe precizia datelor de intrare.
În cazul în care - numărul exact și - valoarea sa aproximativă, o eroare (greșeală) valoarea aproximativă este gradul de proximitate al valorii sale la valoarea sa exactă.
O măsură cantitativă simplă de eroare este eroarea absolută, care este definită ca
După cum se poate observa din formula 1.1.2-1, eroarea absolută are aceleași unități ca valoare. Prin urmare, cea mai mare eroare absolută nu este întotdeauna posibil să se facă o concluzie corectă cu privire la calitatea de apropiere. De exemplu, în cazul în care. dar vorbim despre detaliile mașinii, măsurătorile sunt foarte dur, iar în cazul în care dimensiunea navei, - foarte precis. În acest sens, noțiunea de eroare relativă în care valoarea absolută a erorii este legată de modulul valorilor aproximative ().
Utilizarea erorilor relative convenabilă, în special în sensul că acestea nu depind de valorile unităților de date la scară și măsurare. Eroarea relativă este măsurată ca o fracție sau procent. De exemplu, în cazul în care
,a. apoi, ca și în cazul în care,
Pentru a evalua numeric funcția de eroare, trebuie să cunoașteți regulile de bază de numărare Acțiune erori:
· În adunarea și scăderea numerelor numere absolute de eroare adăuga în sus
· La numerele de înmulțire și împărțire se adaugă reciproc erorile lor relative
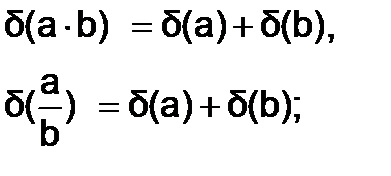
· La exponentiere numărul aproximativ de eroare relativă înmulțită cu exponent
EXEMPLUL 1.1.2-1. Funcția Dana :. Găsiți mărimea absolută și relativă a erorii (eroarea rezultatului efectuării operațiunilor aritmetice), în cazul în care sunt cunoscute valorile, și 1 - numărul exact, eroarea este zero.
Prin definirea astfel, eroarea relativă, se poate găsi o valoare de eroare absolută ca în cazul în care valoarea este determinată de la valori aproximative
Având în vedere că valoarea exactă este, în general necunoscute, formulele de calcul și nu pot fi enumerate mai sus. Prin urmare, în practică, să evalueze limita tipurilor de erori:
în cazul în care - valori cunoscute, care este limita superioară a erorilor absolute și relative, în caz contrar acestea sunt numite - limita absolută și limitarea erorilor relative. Astfel, valoarea curentă variază:
Dacă valoarea este cunoscută, atunci. iar dacă valoarea este cunoscută.
Limitarea eroare absolută a tipului funcției. differentsiruemoyv zonă predeterminată, pentru valori cunoscute ale argumentelor. și la cunoscut argumente limită de eroare absolută. calculat după cum urmează:
și, în consecință, funcția relativă maximă de eroare
În cazul particular al funcției unei variabile (când m = 1):
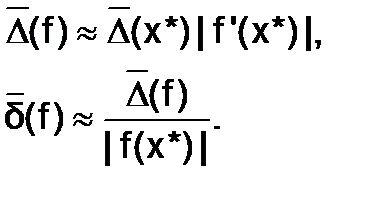
Primer1.1.2-2 .Otsenit eroarea absolută și relativă a numărului aproximativ.
Numărul - un număr transcendental, este infinit fracțiunea non-periodice.
O valoare aproximativă a numărului.
Limita erorii absolute. eroarea relativă a