1.Zadacha de programare liniară.
Principala problemă de programare liniară este de a găsi soluțiile optime pentru funcția obiectiv, care este exprimat în formă liniară.
problemă de programare liniară include funcția obiectiv și sistemul de ecuații în anumite condiții sau restricții care trebuie îndeplinite de către variabile. Funcția obiectiv este definită ca:
unde c 1, c 2, c 3 - coeficienții variabilelor din funcția obiectiv.
x 1, x 2, x 3. - variabile.
Sistemul de ecuații de restricție sau condiție este:
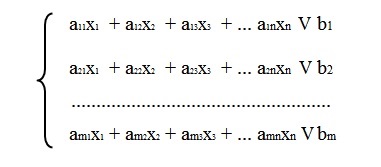
Dacă m = n, atunci sistemul are o singură soluție sau nu există soluții la toate. Dacă m Sistemul Pre de ecuații liniare pot fi scrise sub forma canonică. La începutul înregistrat versiunea originală a (programul de sprijin inițial) decizie, nu neapărat cel mai bun. Apoi, trece la următoarea soluție de referință de Gauss-Jordan. Soluția îmbunătățită rezultată se verifică pe baza unui criteriu optimalitate. După aceea, se trece la următoarea soluție de referință etc. problemă de programare liniară are următoarele proprietăți: 1. În cazul în care sistemul are o extremă, atunci este unic. 2. Setul de toate soluțiile unei probleme de programare liniară este un poliedru convexă. 3. Funcția obiectiv ZLP atinge maximul sau valoarea minimă într-unul din punctele de colț ale poliedru. Dacă funcția obiectiv atinge maximul (minim) în cele două puncte de colt, are o soluții pluralitate ZLP la toate punctele segmentului de legătură aceste puncte de colț. 4. Fiecare punct de colț este o soluție de referință (planul) ZLP.articole similare