Pe atlet de gheață-patinator pentru a atinge o viteză unghiulară mare conectează picioarele, îndreptați trunchiul și trage în sus mâinile pentru a stinge aceeași viteză (în finalul discursului) aruncă mâinile pe părțile laterale. Acest exemplu arată că cinematicii sistemelor mecanice afectează nu numai masele, ci și dispunerea lor reciprocă.
Este cunoscut faptul că în timpul deplasării înainte, o măsură de inerție a corpului este o masă. Întrucât mișcarea de inerție de rotație a corpului este determinată de distribuția greutății acesteia în raport cu axa de rotație, adică, moment de inerție.
De exemplu, celelalte condiții fiind egale (ris.3.19) mișcare de translație, corpul 1 are o masă mai mare, până la oprire, se misca mai corp de lumină 2. Atunci când corpul este mase egale se va opri în mod simultan. În cazul corpurilor de masă egală (ris.3.19), corpul 2, ale căror puncte sunt mai îndepărtate de axa de rotație decât corpul 1, opritorul se rotește mai mult decât corpul 1, a cărui masă este concentrată în apropierea axei de rotație.
Momentul de inerție în raport cu punctul (pol) - valoare scalară, care este numeric egală cu suma tuturor produselor din masa punctelor materiale ale corpului (sistem) de pe pătratul distanței față de pol:
Momentul de inerție în jurul axei - o valoare scalară, care este numeric egală cu suma maselor de toate piesele de puncte importante ale corpului (sistem) de pe pătratul distanței de la axa:
Momentul de inerție în raport cu planul - o valoare scalară, care este numeric egală cu suma maselor de toate piesele de puncte importante ale corpului (sistem) de pe pătratul distanței față de planul:
Un moment de inerție centrifugal al oricărei perechi de axe de coordonate relative - o valoare scalară egală cu suma produselor din fiecare punct de masă în organism pentru a lucra pe axele de coordonate ea sale.
momentele de inerție centrifugale, spre deosebire axial, poate fi negativă și egală cu zero.
Dependențelor dintre momentele de inerție ale unui corp rigid în raport cu axele de coordonate, coordonatele plane și originea au forma:
Momentul de inerție în raport cu o direcție a axei arbitrare.
în cazul în care. . -tsentrobezhnye momente de inerție.
Momentul de inerție al corpului în raport cu o axă predeterminată, pentru axa z exemplu poate fi reprezentat ca:
unde # 961; - raza de inerție în raport cu axa z.
Aceasta determină distanța de la axa razei de girație, (fig. 3.21), care este necesar să se concentreze întreaga greutate corporală ca să aibă același moment de inerție ca și corpul luat în considerare.
Teorema momentelor de inerție în raport cu axe paralele (teorema lui Huygens Steiner)
Momentele de inerție în ceea ce privește diferitele axe vor avea sens diferit. Relația dintre momentele de inerție în raport cu două axe paralele, una dintre care trece prin centrul de masă, determinată în conformitate cu teorema lui Huygens.
Conform acestuia. moment de inerție față de o axă arbitrară egal cu momentul de inerție față de o axă care trece prin centrul de masă al axelor paralele plus produs pătrat greutate distanța între acestea.
. h- unde distanța de la fiecare punct de pe axa z1.
Dovedim această teoremă
Bazat pe determinarea momentului de inerție în jurul axei, putem scrie
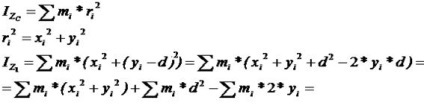
Din formula Huygens văzut că prin îndepărtarea de axa Z1 axa Z v3ulichina Momentul de inerție crește. În consecință, axele toate direcțiile ale celui mai mic momentul de inerție în raport cu o axă care trece prin centrul de masă.