O scurtă descriere a documentului:
Trigonometrie - este una dintre cele mai importante părți, care se studiază în cursul algebra în clasa a 10-a. El a plătit suma destul de generoasă de lecții. Pentru că, în scopul de a înțelege corect trigonometrie, atât în teorie și în practică, necesitatea de a rezolva în mod constant un număr foarte mare de exemple care consolidează teoria și abilitățile va consolida punerea în aplicare a unei lucrări: acasă, de control, de sine, sau pur și simplu se răcească.
Materialul, care descrie și examinează resursa, compilate de către experți, astfel încât să acopere complet subiectul, nu pierdeți un punct important. Se spune că acesta poate fi utilizat în siguranță în pregătirea planurilor, rezumate ale lecțiilor care fac profesorii tineri, fără a eșua.
Mai întâi de toate formulele sunt derivate pătrat de reducere. Putem vedea cât de ușor este de a scăpa de gradul al doilea în cosinusul și sinusului. Pentru elevii pot înțelege în cazul în care a făcut aceste formule, următorul pas crainicul descrie în detaliu toate etapele. În primul rând, merită să ne amintim formula de bază în trigonometria care spune că suma pătratul sinus și cosinus ne dă unitate. Această identitate poate fi afișată separat, iar pătratul sinus și cosinus. Amintindu formula cosinus și sinus argument dublu, puteți vedea în cazul în care există noi reguli.
Este de remarcat că, atunci când orice pas, ne referim la materialul care a fost studiat anterior. Acest lucru indică importanța și interdependenta de subiecte în trigonometrie. În nici un caz nu trebuie ratat sau acel subiect și pentru a începe unul nou. Materialul va fi confuz, deoarece nu este cunoscută a fi, în cazul în care au existat anumite valori și de conversie. Deoarece trigonometria conține un număr mare de formule, fără de care este imposibil să se miște mai departe, ei ar trebui să memoreze și să învețe treptat altele noi. De asemenea, repara materialul necesar pentru a practica și de a dobândi noi competențe care vor fi utile mai târziu, când scrieți lucrarea de testare și semestru.
După aceea, crainicul oferă pentru a rezolva un exemplu similar, în care formula de reducere a sinusului utilizat. Elevii lui poate rezolva în mod independent. Dacă au înțeles exemplul anterior, vă va face față cu acest lucru.
Rezultatul este un alt exemplu mai complex. Dacă se folosește formula sa decizie tangentă. decizie crainic explică în detaliu, și apoi afișează răspunsul.
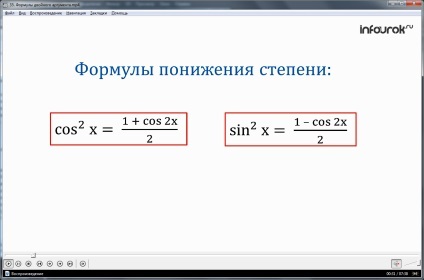
Coborârea formula
cos 2 x = (X pătrat cosinus este egală cu suma unităților din și argumentul semi-dublu cosinus).
= 2 x sin (sinus pătrat X este unitatea de semi-diferență și cosinus argument dublu).
denumite în continuare gradul de formule de reducere.
Deducem aceste formule:
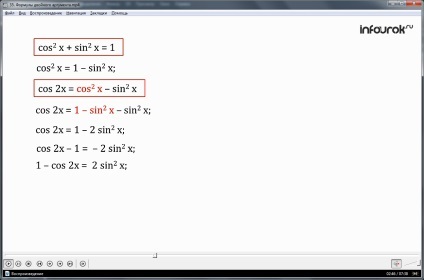
Din formula cos 2 x + sin 2 x = 1, de la 2 x find păcat:
păcatul 2 x = 1-cos 2 x
In formula cos 2x cos 2 x = - păcatul 2 x, 2 x valoare păcat pentru a înlocui 1- cos 2 x și cos 2 x obține - (1- cos 2 x)
dezvăluirea parantezelor obține cos 2 x - cos 2 x 1+
deoarece cos 2 x + cos 2 x in 2 x 2cos cantitate
descoperim că cos 2x = 2 cos 2 x - 1.
cos 2x = x cos 2 - sin 2 x = cos 2 x - (1-cos 2 x) = 2 cos 2 x - 1.
De aici exprima cos 2 x
cos 2x +1 = 2 cos 2 x
cos 2 x = (X pătrat cosinus este egală cu suma unităților din și argumentul semi-dublu cosinus).
Am luat primul grad de formula de reducere pentru cos 2 x.
În mod similar, a doua și deriva o formulă pentru gradul de reducere 2 x păcat:
Din formula cos 2 x + sin 2 x = 1, de la 2 x cos descoperim:
cos 2 x = 1 - 2 x păcat
In formula cos 2x cos 2 x = - sin 2 x, valoarea x CoS 2:
înlocuind 1 - păcatul 2 x
Obținem 1 - păcatul 2 x 2 x păcat
Deoarece -sin 2 x 2 x -sin valoare da -2 păcatului 2 x,
Obținem că cos 2x = 1 -2 păcat 2 x.
exprimă De aici păcatul 2 x:
transfer de unități cu semn opus
cos 2x-1 = -2 păcat 2 x
modificări semn
1- cos 2x = 2 sin 2 x
se împarte la 2 ambele părți:
= 2 x sin (sinus pătrat X este unitatea de semi-diferență și cosinus argument dublu).
Amintiți-vă, cu formula pe care ne-am referit ca gradul de formule de reducere.
Acest nume a fost dat din cauza faptului că partea stângă a ambelor identități conține al doilea cosinusul și sinusul, iar pe partea dreapta - primul grad, și anume scăderea observată în severitate.
Luați în considerare soluția exemplelor folosind gradul de formule de reducere.
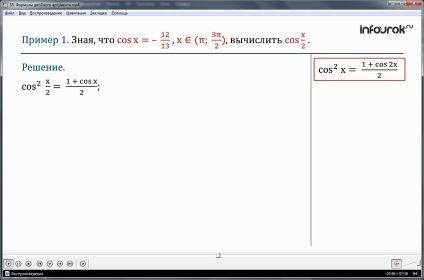
Exemplul 1. Știind că cosx = - și hε (π;) (X aparține unui interval de pi pi la trei de doi), se calculează cos.
Vom folosi gradul de reducere a formula
X patrat cos cosinus x = 2,. obținem:
cu condiția COSX = - înlocuind datele în formulă, avem:
cos = 2. face calculele de pe partea dreaptă a expresiei, vom obține
cos = 2. extrage rădăcina pătrată. obținem
Prin starea π x. Prin urmare. Acest lucru înseamnă că argumentul X, împărțit la doi aparține al doilea trimestru, în cazul în care cosinusul este negativ. Prin urmare, cos = -.
Raspuns: cos = -.
Exemplul 2. Știind că cosx = - și hε (π;)
(X aparține unui interval de pi pi la trei de doi), se calculează păcatul.
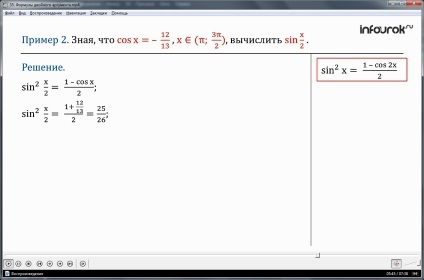
Decizie. Noi folosim gradul de reducere a formulei păcatului 2 x =
2 = sin, deoarece prin ipoteza cosx = -
Avem: păcat 2 =. Am extrage rădăcina pătrată, și obținem
Prin starea π x. Prin urmare. Acest lucru înseamnă că argumentul X, împărțit la doi aparține al doilea trimestru, în cazul în care sinusul este pozitiv. De aceea, păcatul =.
Exemplul 3. Știind că cosx = - și hε (π;) (X aparține unui interval de pi pi la trei de doi), se calculează tg.
Decizie. Știind că tangenta X - X este raportul dintre sinusul la cosinusul X, avem
Exemplele 1 și 2, descoperim că păcatul = și cos = -. prin urmare
Raspuns: tg = -5.