proporționalitate directă este un caz special al funcției $ y liniar = kx + b $ la $ b = $ 0 ° C. Numărul de $ k $ se numește coeficientul de proporționalitate.
Un exemplu de proporționalitate directă poate servi ca legea a doua a lui Newton: accelerare a corpului este direct proporțională cu forța aplicată l:
greutate Există - factor de proporționalitate.
Investigarea directă proporționalitate funcției $ f (x) = kx $, iar graficul acesteia
În primul rând, să ia în considerare funcția $ f \ stânga (x \ dreapta) = $ kx, în cazul în care $ k> 0 $.
- Domeniul de definiție - toate numerele.
- Intervalul de valori - toate numerele.
- $ F \ stânga (-x \ dreapta) = - kx = -f (x) $. Funcția de proporționalitate directă este ciudat.
- Funcția trece prin origine.
- $ F '\ x \ stânga (dreapta) =' = k> 0 $. Prin urmare, această funcție este în creștere pe domeniul său. Nu există puncte extreme.
- $ F ^ \ din stânga (x \ dreapta) = k „= 0 $. Prin urmare, funcția nu are puncte de inflexiune.
- $ _ Kx \> = - \ infty $, $ _ kx \> = + \ infty $
- Graph (Fig. 1).
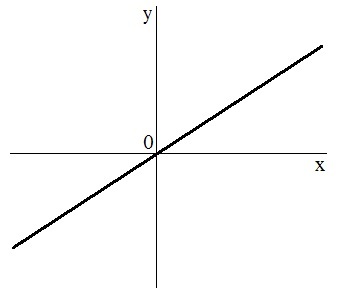
Fig. 1. Graficul de $ y = kx $, atunci $ k> 0 $
Acum, ia în considerare funcția $ f \ stânga (x \ dreapta) = $ kx, în cazul în care $ k
- Domeniul de definiție - toate numerele.
- Intervalul de valori - toate numerele.
- $ F \ stânga (-x \ dreapta) = - kx = -f (x) $. Funcția de proporționalitate directă este ciudat.
- Funcția trece prin origine.
- $ F '\ stânga (x \ dreapta) =' = k
- $ F ^ \ din stânga (x \ dreapta) = k „= 0 $. Prin urmare, funcția nu are puncte de inflexiune.
- $ _ Kx \> = + \ infty $, $ _ kx \> = - \ infty $
- Graph (Fig. 2).
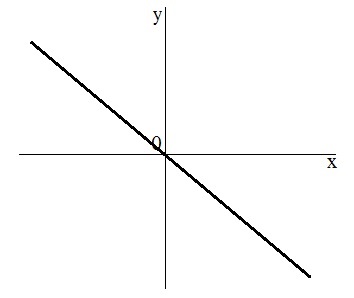
Fig. 2. Graficul de $ y = $ kx, pentru $ k
Important: pentru a reprezenta grafic funcția $ y = kx $ suficient pentru a găsi unul care este diferită de punctul de origine al $ \ stânga (x_0, \ y_0 \ dreapta) $ și trage o linie dreaptă prin punctul și originea.